Figure 8.2:
(a) Consider a merry-go-round that rotates at constant angular velocity 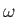 . (Picture by Seattle Parks and Recreation.) (b) In a top-down view, the velocity vector,
. (Picture by Seattle Parks and Recreation.) (b) In a top-down view, the velocity vector, 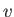 , for a point on the merry-go-round is tangent to the circle that contains it; the circle is centered on the axis of rotation and the acceleration vector,
, for a point on the merry-go-round is tangent to the circle that contains it; the circle is centered on the axis of rotation and the acceleration vector, 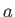 , points toward its center.
, points toward its center.
 |
To understand the issues, consider the simple case of a spinning merry-go-round, as shown in Figure 8.2(a). Its orientation at every time can be described by 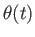 ; see Figure 8.2(b). Let
; see Figure 8.2(b). Let 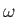 denote its angular velocity:
denote its angular velocity:
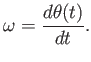 |
(8.10) |
By default, 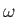 has units of radians per second. If
has units of radians per second. If
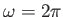 , then the rigid body returns to the same orientation after one second.
, then the rigid body returns to the same orientation after one second.
Assuming
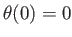 and
and 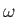 is constant, the orientation at time
is constant, the orientation at time 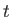 is given by
is given by
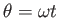 . To describe the motion of a point on the body, it will be convenient to use polar coordinates
. To describe the motion of a point on the body, it will be convenient to use polar coordinates 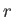 and
and 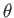 :
:
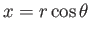 and and 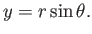 |
(8.11) |
Substituting
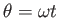 yields
yields
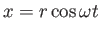 and and 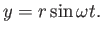 |
(8.12) |
Taking the derivative with respect to time yields8.2
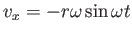 and and 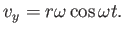 |
(8.13) |
The velocity is a 2D vector that when placed at the point is tangent to the circle that contains the point 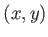 ; see Figure 8.2(b).
; see Figure 8.2(b).
This makes intuitive sense because the point is heading in that direction; however, the direction quickly changes because it must move along a circle. This change in velocity implies that a nonzero acceleration occurs. The acceleration of the point 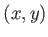 is obtained by taking the derivative again:
is obtained by taking the derivative again:
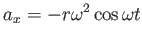 and and 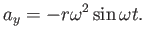 |
(8.14) |
The result is a 2D acceleration vector that is pointing toward the center (Figure 8.2(b)), which is the rotation axis. This is called centripetal acceleration. If you were standing at that point, then you would feel a pull in the opposite direction, as if nature were attempting to fling you away from the center. This is precisely how artificial gravity can be achieved in a rotating space station.
Steven M LaValle
2020-01-06


![]() ; see Figure 8.2(b). Let
; see Figure 8.2(b). Let ![]() denote its angular velocity:
denote its angular velocity:
![]() and
and ![]() is constant, the orientation at time
is constant, the orientation at time ![]() is given by
is given by
![]() . To describe the motion of a point on the body, it will be convenient to use polar coordinates
. To describe the motion of a point on the body, it will be convenient to use polar coordinates ![]() and
and ![]() :
:
![]() is obtained by taking the derivative again:
is obtained by taking the derivative again: