
Next: The phase space Up: 8.3.2 Numerical simulation Previous: Runge-Kutta integration Contents Index
The second problem from (8.20) is to determine an expression for
![]() . This is where the laws of physics, such as the acceleration of rigid bodies due to applied forces and gravity. The most common case is time-invariant dynamical systems, in which
. This is where the laws of physics, such as the acceleration of rigid bodies due to applied forces and gravity. The most common case is time-invariant dynamical systems, in which ![]() depends only on the current state and not the particular time. This means each component
depends only on the current state and not the particular time. This means each component ![]() is expressed as
is expressed as
Here is a simple, one-dimensional example of a state transition equation:
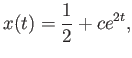 |
(8.28) |
Steven M LaValle 2020-01-06