
Next: Types of vection Up: 8.4 Mismatched Motion and Previous: 8.4 Mismatched Motion and Contents Index
 |
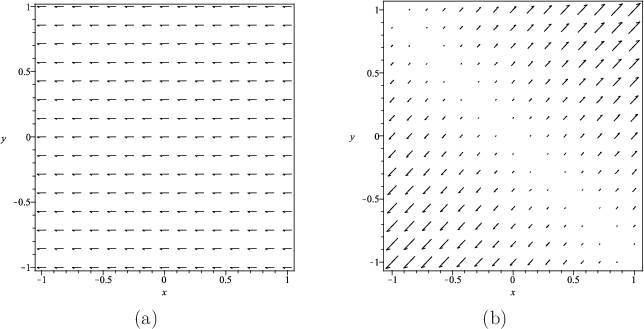 |
Recall from Section 6.2, that the human visual system has neural structures dedicated to detecting the motion of visual features in the field of view; see Figure 8.13. It is actually the images of these features that move across the retina. It is therefore useful to have a mathematical concept that describes the velocities of moving points over a surface. We therefore define a vector field, which assigns a velocity vector at every point along a surface. If the surface is the ![]() plane, then a velocity vector
plane, then a velocity vector
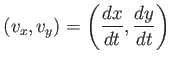 |
(8.32) |
| (8.33) |
| (8.34) |
To most accurately describe the motion of features along the retina, the vector field should be defined over a spherical surface that corresponds to the locations of the photoreceptors. Instead, we will describe vector fields over a square region, with the understanding that it should be transformed onto a sphere for greater accuracy.
Steven M LaValle 2020-01-06