
Next: Filtering Up: 9.2 Tracking 3D Orientation Previous: Tilt correction Contents Index
The remaining drift error component is detected by a ``compass'', which outputs a vector that lies in the world ![]() plane and always points ``north''. Suppose this is
plane and always points ``north''. Suppose this is
![]() . Once again, the sensor output occurs in the coordinate frame of the body, and needs to be transformed by
. Once again, the sensor output occurs in the coordinate frame of the body, and needs to be transformed by
![]() . The difference between
. The difference between ![]() and the
and the ![]() axis is the resulting yaw drift error.
axis is the resulting yaw drift error.
 |
As in the case of the ``up'' sensor, there is no ``compass'' in the real world.
Instead, there is a magnetometer, which measures a 3D magnetic field vector:
![]() . Suppose this is used to measure the Earth's magnetic field. It turns out that the field vectors do not ``point'' to the North pole.
The Earth's magnetic field produces 3D vectors that generally do not lie in the horizontal plane, resulting in an inclination angle. Thus, the first problem is that the sensor output must be projected into the
. Suppose this is used to measure the Earth's magnetic field. It turns out that the field vectors do not ``point'' to the North pole.
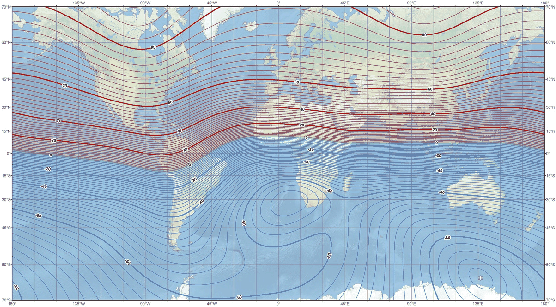
The Earth's magnetic field produces 3D vectors that generally do not lie in the horizontal plane, resulting in an inclination angle. Thus, the first problem is that the sensor output must be projected into the ![]() plane. Residents of Ecuador may enjoy magnetic field vectors that are nearly horizontal; however, in Finland they are closer to vertical; see Figure 9.6. If the magnetic field vector is close to vertical, then the horizontal component may become too small to be useful.
plane. Residents of Ecuador may enjoy magnetic field vectors that are nearly horizontal; however, in Finland they are closer to vertical; see Figure 9.6. If the magnetic field vector is close to vertical, then the horizontal component may become too small to be useful.
Another issue is that the projected vector in the horizontal plane does not point north, resulting in a declination angle; this is the deviation from north. Fortunately, reference to the true north is not important. It only matters that the sensor output is recorded in the registration stage to provide a fixed yaw reference.
The most significant problem is that the magnetometer measures the vector sum of all magnetic field sources. In addition to the Earth's field, a building generates its own field due to ferromagnetic metals. Furthermore, such materials usually exist on the circuit board that contains the sensor. For this case, the field moves with the sensor, generating a constant vector offset. Materials that serve as a source of magnetic fields are called hard iron. Other materials distort magnetic fields that pass through them; these are called soft iron. Magnetometer calibration methods mainly take into account offsets due to hard-iron bias and eccentricities due to soft-iron bias [93,157].
After these magnetometer calibrations have been performed, the yaw drift error can be estimated from most locations with a few degrees of accuracy, which is sufficient to keep yaw errors from gradually accumulating. There are still problems. If a strong field is placed near the sensor, then the readings become dependent on small location changes. This could cause the measured direction to change as the rigid body translates back and forth. Another problem is that in some building locations, vector sum of the Earth's magnetic field and the field generated by the building could be approximately zero (if they are of similar magnitude and pointing in opposite directions). In this unfortunate case, the magnetometer cannot produce useful outputs for yaw drift error detection.
Steven M LaValle 2020-01-06