
Next: Where are the lenses? Up: 11.1 The Physics of Previous: Diffraction Contents Index
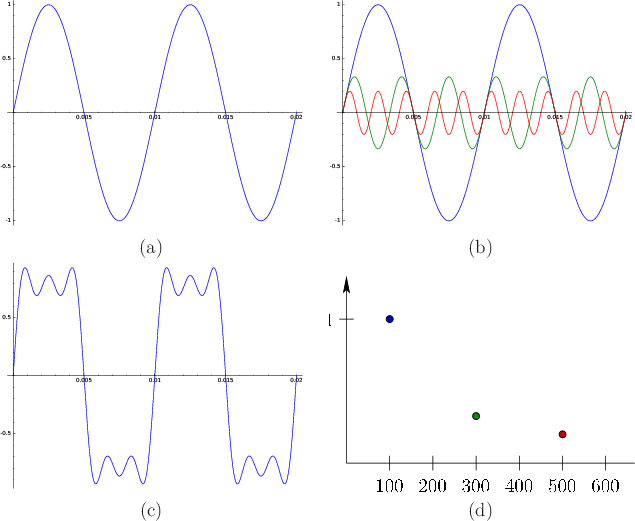 |
Spectral decompositions were important for characterizing light sources and reflections in Section 4.1. In the case of sound, they are even more important. A sinusoidal wave, as shown in Figure 11.3(a), corresponds to a pure tone, which has a single associated frequency; this is analogous to a color from the light spectrum. A more complex waveform, such the sound of a piano note, can be constructed from a combination of various pure tones. Figures 11.3(b) to 11.3(d) provide a simple example. This principle is derived from Fourier analysis, which enables any periodic function to be decomposed into sinusoids (pure tones in our case) by simply adding them up. Each pure tone has a particular frequency, amplitude or scaling factor, and a possible timing for its peak, which is called its phase. By simply adding up a finite number of pure tones, virtually any useful waveform can be closely approximated. The higher-frequency, lower-amplitude sinusoids are often called higher-order harmonics; the largest amplitude wave is called the fundamental frequency. The plot of amplitude and phase as a function of frequency is obtained by applying the Fourier transform, which will be briefly covered in Section 11.4.
Steven M LaValle 2020-01-06