
Next: Correlation coefficient Up: 12.4 Experiments on Human Previous: Formulating a hypothesis Contents Index
Unfortunately, the scientist is not able to perform the same experiment at the same time on all people. She must instead draw a small set of people from the population and make a determination about whether the hypothesis is true. Let the index ![]() refer to a particular chosen subject, and let
refer to a particular chosen subject, and let ![]() be his or her response for the experiment; each subject's response is a dependent variable. Two statistics are important for combining information from the dependent variables: The mean,
be his or her response for the experiment; each subject's response is a dependent variable. Two statistics are important for combining information from the dependent variables: The mean,
![$\displaystyle \hat{\mu}= \frac{1}{n} \sum_{j=1}^n y[j] ,$](img1074.gif) |
(12.3) |
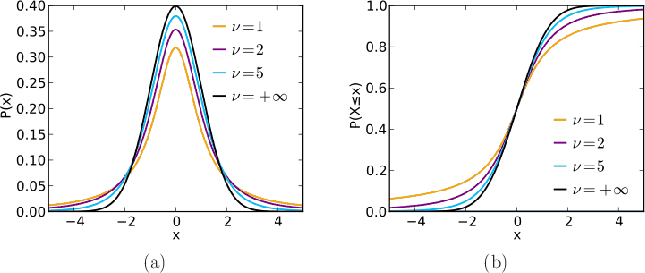 |
To test the hypothesis, Student's t-distribution (``Student'' was William Sealy Gosset) is widely used, which is a probability distribution that captures how the mean ![]() is distributed if
is distributed if ![]() subjects are chosen at random and their responses
subjects are chosen at random and their responses ![]() are averaged; see Figure 12.5. This assumes that the response
are averaged; see Figure 12.5. This assumes that the response ![]() for each individual
for each individual ![]() is a normal distribution (called Gaussian distribution in engineering), which is the most basic and common probability distribution. It is fully characterized in terms of its mean
is a normal distribution (called Gaussian distribution in engineering), which is the most basic and common probability distribution. It is fully characterized in terms of its mean ![]() and standard deviation
and standard deviation ![]() . The exact expressions for these distributions are not given here, but are widely available; see [125] and other books on mathematical statistics for these and many more.
. The exact expressions for these distributions are not given here, but are widely available; see [125] and other books on mathematical statistics for these and many more.
The Student's t test [319] involves calculating the following:
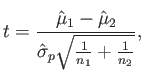 |
(12.5) |
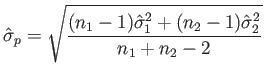 |
(12.6) |
The binary outcome might not be satisfying enough. This is not a problem because difference in means,
![]() , is an estimate of the amount of change that applying
, is an estimate of the amount of change that applying ![]() had in comparison to
had in comparison to ![]() . This is called the average treatment effect. Thus, in addition to determining whether the
. This is called the average treatment effect. Thus, in addition to determining whether the ![]() is true via the t-test, we also obtain an estimate of how much it affects the outcome.
is true via the t-test, we also obtain an estimate of how much it affects the outcome.
Student's t-test assumed that the variance within each group is identical. If it is not, then Welch's t-test is used [350]. Note that the variances were not given in advance in either case. They are estimated ``on the fly'' from the experimental data. Welch's t-test gives the same result as Student's t-test if the variances happen to be the same; therefore, when in doubt, it may be best to apply Welch's t-test. Many other tests can be used and are debated in particular contexts by scientists; see [125].
Steven M LaValle 2020-01-06