Consider the following 3D triangle,
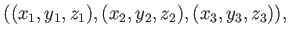 |
(3.2) |
in which its vertex coordinates are expressed as generic constants.
Let 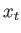 ,
, 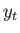 , and
, and 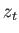 be the amount we would like to change the triangle's position, along the
be the amount we would like to change the triangle's position, along the 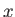 ,
, 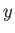 , and
, and 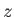 axes, respectively. The operation of changing position is called translation, and it is given by
axes, respectively. The operation of changing position is called translation, and it is given by
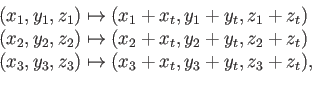 |
(3.3) |
in which
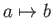 denotes that
denotes that 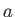 becomes replaced by
becomes replaced by 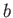 after the transformation is applied. Applying (3.3) to every triangle in a model will translate all of it to the desired location. If the triangles are arranged in a mesh, then it is sufficient to apply the transformation to the vertices alone. All of the triangles will retain their size and shape.
after the transformation is applied. Applying (3.3) to every triangle in a model will translate all of it to the desired location. If the triangles are arranged in a mesh, then it is sufficient to apply the transformation to the vertices alone. All of the triangles will retain their size and shape.
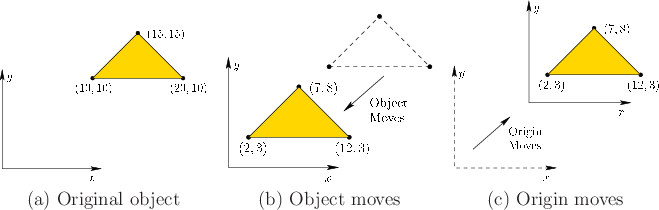
Figure 3.4:
Every transformation has two possible interpretations, even though the math is the same. Here is a 2D example, in which a triangle is defined in (a). We could translate the triangle by 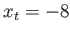 and
and 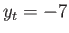 to obtain the result in (b). If we instead wanted to hold the triangle fixed but move the origin up by
to obtain the result in (b). If we instead wanted to hold the triangle fixed but move the origin up by 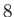 in the
in the 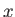 direction and
direction and 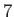 in the
in the 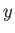 direction, then the coordinates of the triangle vertices change the exact same way, as shown in (c).
direction, then the coordinates of the triangle vertices change the exact same way, as shown in (c).
 |
Steven M LaValle
2020-01-06

![]() ,
, ![]() , and
, and ![]() be the amount we would like to change the triangle's position, along the
be the amount we would like to change the triangle's position, along the ![]() ,
, ![]() , and
, and ![]() axes, respectively. The operation of changing position is called translation, and it is given by
axes, respectively. The operation of changing position is called translation, and it is given by
