
Next: Combining rotations Up: 3.2 Changing Position and Previous: The 3D case Contents Index
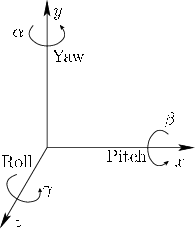 |
One of the simplest ways to parameterize 3D rotations is to construct them from ``2D-like'' transformations, as shown in Figure 3.7. First consider a rotation about the ![]() -axis. Let roll be a counterclockwise rotation of
-axis. Let roll be a counterclockwise rotation of ![]() about the
about the ![]() -axis. The rotation matrix is given by
-axis. The rotation matrix is given by
Similarly, let pitch be a counterclockwise rotation of ![]() about the
about the ![]() -axis:
-axis:
Finally, let yaw be a counterclockwise rotation
of ![]() about the
about the ![]() -axis:
-axis:
Steven M LaValle 2020-01-06