
Next: 3.5 Chaining the Transformations Up: 3.4 Viewing Transformations Previous: Orthographic projection Contents Index
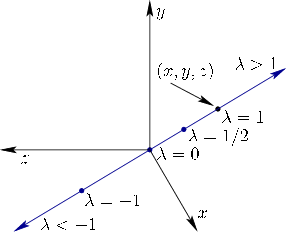 |
Instead of using orthographic projection, we define a perspective projection. For each point ![]() , consider a line through the origin. This is the set of all points with coordinates
, consider a line through the origin. This is the set of all points with coordinates
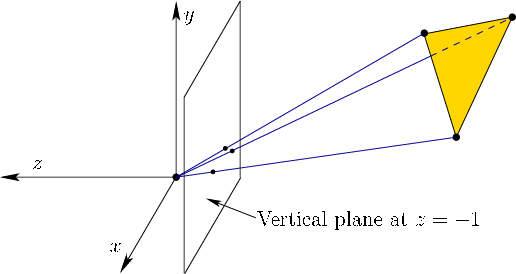 |
Now we can place a planar ``movie screen'' anywhere in the virtual world and see where all of the lines pierce it. To keep the math simple, we pick the ![]() plane to place our virtual screen directly in front of the eye; see Figure 3.17. Using the third component of (3.39), we have
plane to place our virtual screen directly in front of the eye; see Figure 3.17. Using the third component of (3.39), we have
![]() , implying that
, implying that
![]() .
Using the first two components of (3.39), the coordinates for the points on the screen are calculated as
.
Using the first two components of (3.39), the coordinates for the points on the screen are calculated as ![]() and
and ![]() .
Note that since
.
Note that since ![]() and
and ![]() are scaled by the same amount
are scaled by the same amount ![]() for each axis, their aspect ratio is preserved on the screen.
for each axis, their aspect ratio is preserved on the screen.
More generally, suppose the vertical screen is placed at some location ![]() along the
along the ![]() axis. In this case, we obtain more general expressions for the location of a point on the screen:
axis. In this case, we obtain more general expressions for the location of a point on the screen:
This is all we need to project the points onto a virtual screen, while respecting the scaling properties of objects at various distances. Getting this right in VR helps in the perception of depth and scale, which are covered in Section 6.1. In Section 3.5, we will adapt (3.40) using transformation matrices. Furthermore, only points that lie within a zone in front of the eye will be projected onto the virtual screen. Points that are too close, too far, or in outside the normal field of view will not be rendered on the virtual screen; this is addressed in Section 3.5 and Chapter 7.
Steven M LaValle 2020-01-06