3.5 Chaining the Transformations
This section links all of the transformations of this chapter together while also slightly adjusting their form to match what is currently used in the VR and computer graphics industries. Some of the matrices appearing in this section may seem unnecessarily complicated. The reason is that the expressions are motivated by algorithm and hardware issues, rather than mathematical simplicity. In particular, there is a bias toward putting every transformation into a 4 by 4 homogeneous transform matrix, even in the case of perspective projection which is not even linear (recall (3.40)). In this way, an efficient matrix multiplication algorithm can be iterated over the chain of matrices to produce the result.
The chain generally appears as follows:
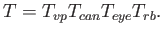 |
(3.41) |
When 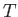 is applied to a point
is applied to a point 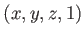 , the location of the point on the screen is produced. Remember that these matrix multiplications are not commutative, and the operations are applied from right to left. The first matrix
, the location of the point on the screen is produced. Remember that these matrix multiplications are not commutative, and the operations are applied from right to left. The first matrix 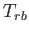 is the rigid body transform (3.23) applied to points on a movable model. For each rigid object in the model,
is the rigid body transform (3.23) applied to points on a movable model. For each rigid object in the model, 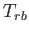 remains the same; however, different objects will generally be placed in various positions and orientations. For example, the wheel of a virtual car will move differently than the avatar's head. After
remains the same; however, different objects will generally be placed in various positions and orientations. For example, the wheel of a virtual car will move differently than the avatar's head. After 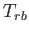 is applied,
is applied, 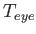 transforms the virtual world into the coordinate frame of the eye, according to (3.36). At a fixed instant in time, this and all remaining transformation matrices are the same for all points in the virtual world. Here we assume that the eye is positioned at the midpoint between the two virtual human eyes, leading to a cyclopean viewpoint. Later in this section, we will extend it to the case of left and right eyes so that stereo viewpoints can be constructed.
transforms the virtual world into the coordinate frame of the eye, according to (3.36). At a fixed instant in time, this and all remaining transformation matrices are the same for all points in the virtual world. Here we assume that the eye is positioned at the midpoint between the two virtual human eyes, leading to a cyclopean viewpoint. Later in this section, we will extend it to the case of left and right eyes so that stereo viewpoints can be constructed.
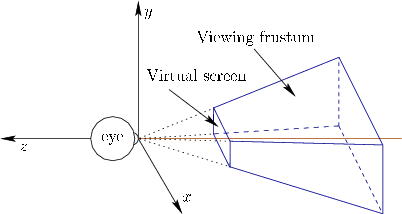
Figure 3.18:
The viewing frustum.
 |
Subsections
Steven M LaValle
2020-01-06
