Path Planning in a Topologist's World
Computer Science 576 FINAL PROJECT Spring 1999
Lewis
C. Hill II lchill@iastate.edu
Project Description
This project has explored path planning in topologically identified
worlds. The robot is a holonomic 2D rigid body with rotation which
moves in the configuration space (R^2 x S^1). The original project proposal
indicated that this application would use randomized roadmap planning,
however preliminary findings lead the developer to use random tree methods
(RRT's). Proposal.
The task of path planning for the robot used in this project can be
addressed well with traditional methods for non-identified worlds.
The identified world requires key modifications to the 'standard' RRT algorithm.
The RRT
method must be modified to correctly compute distances between two
identified points. This method must also correctly add and connect nodes
'around' the boundaries of the identified world. Further, these modifications
must be written such that combinations of identifications (i.e. reverse
and normal identification for X and Y axis, respectively) work successfully.
Approach
The application developed for this project is written in object oriented
C++. The user interface is generated through
Silicon Graphics RapidApp development kit and uses OpenGL graphics. The
application allows the user to interactively construct the obstacle region
and robot. The user can also set initial and final configuration.
The user may select identification options for the world. They may select
for both the X and Y axis to have no identification, normal identification,
or reverse identification. The user can enable or disable the display of
the RRT tree and/or final path. Also, the user may interactively set epsilon
for new tree node interpolation. The application is pictured here.
The planning aspects of this project are implemented in a class Planner.
Planner users LEDA objects to store the obstacle region, initial and final
robot configuration, rapid tree, and final pathway information. Planner
also maintains the state of current world identifications. Additional Planner
methods include modified cartesian distance (d = (dx^2 + dy^2 + scalefactor
*dtheta^2)^.5). The scalefactor is user adjustable to change the
impact of a rotation on the distance between two configurations. Planner
features another method identified_distance. Identified_distance
returns the minimum of three distances: the distance (as described above)
between two configurations, the distance between the first point and an
identified version of the second point, or the distance between the second
point and the identified version of the first point. Examples for normal
identification and reverse identification are
shown here. The identified distance function also returns the identified
version of a points if the nearest pair is identified. To determine
the new point to add to the configuration, we interpolate from the nearest
point toward the identified point.
Planner also implements the identify point function. This function
maps points which are just beyond the normal boundary for X or Y back into
the appropriate location. A one dimensional example would be, on
a number line form 0-10, the number 13 would be re-mapped under normal
identification to [(13-10)] = 3 and under reverse identification to [(10-13)+10]
= 7.
Effectiveness
This method works well for many obstacle regions. There is an
increased computational load over traditional RRT's for identified distance
checks because each distance is computed as many as three times.
In determining the effectiveness of this algorithm, it is beneficial
to study the impact of the various identifications on the constructed tree
and final path. The computed examples section illustrates several
trees and present short descriptions of the characteristics of the trees
and the final path. In general though, where an identified pathway
is available, the algorithm will find it.
The option to weight rotations more or less heavily than distance translations
does affect the final pathway. The algorithm does require more time
with high rotation penalty imposed, but it does generate a pathway with
less rotations.
Computed Examples
This robot planning application is flexible in allowing the user to
experiment with the configuration space. The following examples show
the performance of the system on the same obstacle region for several different
identification settings. The examples indicate the random tree and selected
path. Links are also provided to animations of the pathways.
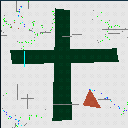
| No Identification
Normal World |
|
movie
|
| High Rotation Penalty (No Identification)
Normal World |

|
movie
|
| Tough World (No Identification)
Normal World
Did not find a solution. |

|
movie
|
| Forward X Identification, No Y Identification
Cylindrical World |

|
movie
|
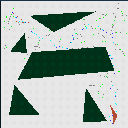
| X and Y Forward Identification
Toroidal World |
|
movie
|
| X and Y Reversed Identification
Projective Plane |
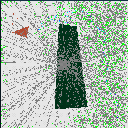
|
movie
|
| X Normal and Reversed Identification, Y Reversed Identification
*This one is wierd. It's actually a bug, but the test considers BOTH
the reversed and normal identified X coordiante as well as the reversed
Y coordiante. This is hereby dubbed the ELCHILL world. |

|
movie
|
Implementation Files
Source Code:
Input Data Files:
There are no example data files. Users may construct their own
arbitrary world through built-in polygon construction methods.






