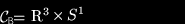The problem of this project was to implement different variations
of RRT-planners in a 3D world. Two different robots were implemented, robot
A with 2 DOF and robot B with 4 DOF, this gives us the following configuration
spaces:

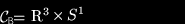
The robot B in addition to being able to translate in x,y and z directions
it can rotate around the y-axis.
The model of this project is a standard holonomic model, but the user
is able to specify the inputs to the robots. By specifying inputs the user
can add constraints to the model, like forward and downward only helicopter
or forward and left turn only helicopter. This type of kinematic constraints
still makes the problem holonomic and small-time controllable.
What makes this project difficult is the transition from 4D configuration
space to a 3D world space. Going from a un-visualizable 4D to 3D was a
problem in implementing this
project.
The application is written in C++ using object oriented techniques.
The graphical interface is based on openGL and vrJuggler.
vrJuggler is a platform for developing VR applications that allows the
user to simulate virtual environments on regular SGI workstations. For
collision detection the PQP-toolkit
is used. The use of PQP along with LEDA
allows for flexible and 'easy' integration of the course framework for
motion planning.
The approach was to extend the application being developed for CpE
575 Virtual Reality to also include motion planning. This application enables
the user to create a 'virtual maze' by sketching it in 2D then transforming
this sketch into 3D, then allow the user to navigate in the created maze
and modify it further. (The final report for CpE 575 can be found here).
This was done by allowing the user to place the two robots A and B in the
scene. Then the user was able to choose from the RRT-implementations provided
in the course framework, the RRT-implementations are: RRT, RRTGoalBias,
RRTCon, RRTExt, RRTConCon, RRTExtExt, RRTExtCon. This allows the user to
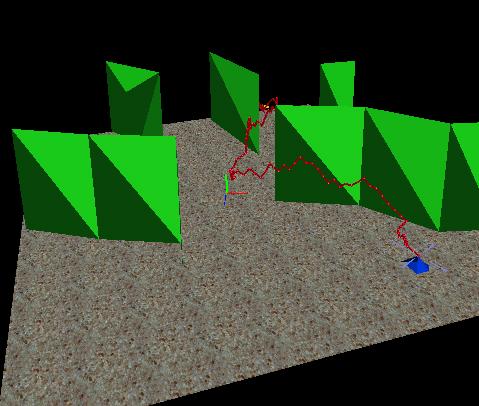
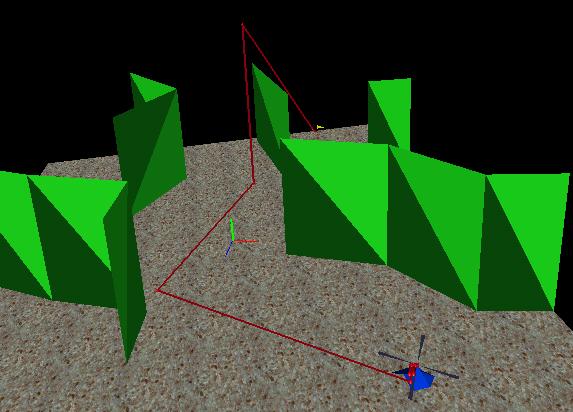
run the different RRT's on the same geometry and observe the different
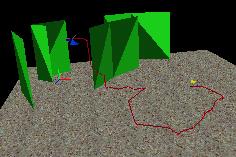
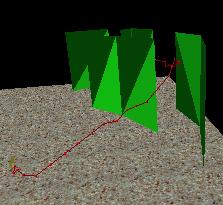
behaviors. The user is also able to show all the nodes generated by the
RRT, show an successful path and animate an successful path. (fig.1).

In order to make the course framework to work with a 3D environment
mode additions and modifications were necessary for the framework. First,
the World-class was extended with an WorldPQP class. This new class
essentially handled collision detection with the scene, this was done by
querying the PQP objects for collision distance. Then the Problem-class
was extended with an Problem3D class that handled reading inputs corresponding
to the 2D inputs for robot A, and the 4 D inputs for robot B. Finally,
the Model-class had to be extended with a Model3D-class. This new
class included the following changes:
Metric:
{
double dphi = min(fabs(x1[3]-x2[3]),2.0*PI - fabs(x1[3]-x2[3]));
double rho;
rho = sqrt(sqr(x1[0] - x2[0]) + sqr(x1[1] - x2[1]) + sqr(x1[2] - x2[2])
+ sqr(20/PI*dphi));
return rho;
}
State Transition Equations:
{
vector dx(4);
dx[0] = Speed*u[0]* cos(x[3]);
dx[1] = Speed*u[1];
dx[2] = Speed*u[0]*sin(x[3]);
dx[3] = u[3];
return dx;
}