
Zuojun Shen


RRT based method can be used to solve highly constrained nonlinear dynamic problem. But the dynamic charateristics of the specific system should be handled properly in using the RRT method. For complicated dynamic systems like the Entry Guidance problem of spacecraft, the metric plays a key role in using the RRT. In the Entry Guidance problem, bank angle is used as the solo control to guide the spacecraft to reach the predetermined TAEM(terminal area energy management) point while satisfying all trajectory constraints. One way to achieve this is using paramemter optimization method. The bank angle is parameterized as a piecewise linear function of time. The nodal values of the bank angle and the terminal time Tf are used as parameters to be solved and to optimize a performance index such as Tf itself,or the accumulated heat on the body of the spacecraft,etc.
But this approach is really time consuming and requires much human-interfering. Each constraint means an additional equation or inequality to be added to the already complicated dynamic system. Compared with this method,RRT based path planning shows great power in handling constraints and improving path-seraching robustness. However the shortage,if there is,is that we need to design a smart decision maker that can always drive the object closer to its goal through the constraint-satisfied vecter space.This decision maker is the metirc used in the RRT based method. To design a good metric,first we need to study the underlying physical essence. It turns out that Entry Guidance problem is too complicated to be chosen as starting point of the reserach. Thus two classical problems, the hitting and rendezvous problems,are studied. Proper metrics have been designed for this two problems in this final project. The result may provide some clue for how to design a good metric for other more complicated systems.
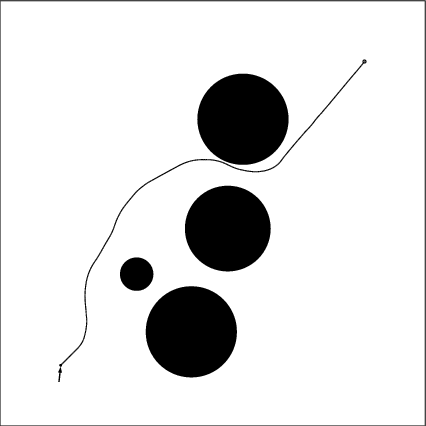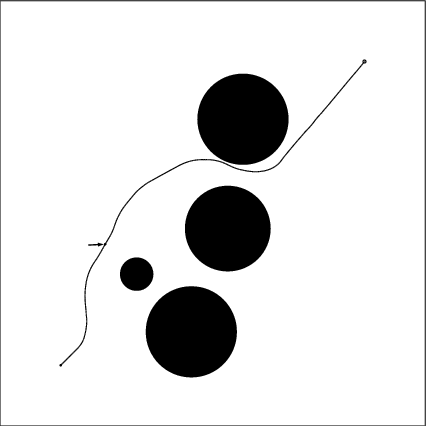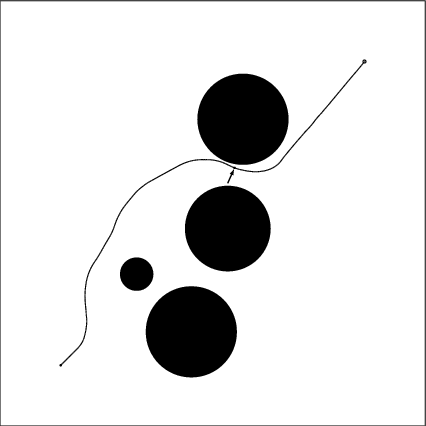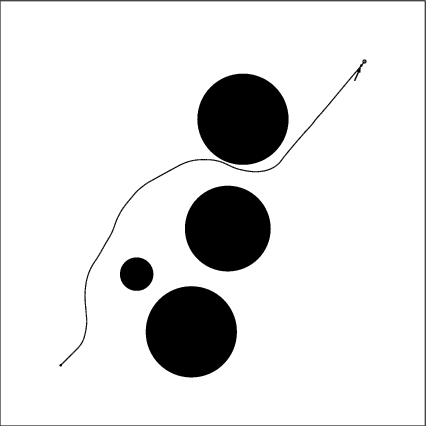
There is a point mass robot with a force acting on it. The force is constant in its magnitude while the direction of the force is controllable. The maximum rate of changing the force direction is 120 degree per second. The point mass is subjected to drag force which is in the opposite direction of the velocity. The drag force is linearly proportional to the velocity.The initial location is (0,0) and the goal location is (100,100). The area in which the robot is allowed to maneuver is a square area ranging from x=-20 to x=120 and from y=-20 to y=120.
The dynamic equations for the point mass robot is:
x' = Vx
Vx' = cos(u) - Vx/7
y' = Vy
Vy' = sin(u) - Vy/7
where the 'u' represents the force direction measured from positive x axis counterclock.The force magnitude is assumed to be one unit. The Vx/7 and Vy/7 are drag force in x and y direction respectively. It is easy to verify that the drag equals to the pushing force when the velocity is 7.
Task 1: Hitting the Target
There are 4 circular obstacles in the area. We want the robot to hit the goal using the RRT algorithm. As comparison, by using the optimization algorithm Fortran code FFSQP(Fortran Feasible Sequential Quadratic Programming) developed by Zhou et al,an optimal solution is shown. The arrow in the animation points along the force direction. The piecewise linear variation of the force dirction control history is also recorded. The hitting time and 19 control nodal values are chosen to be optimized using FFSQP for this solution. 353 iterations of whole path integration are computed at the cost of 7 minutes of Alpha 500 workstation terminal time.
RRT Soluion
First,we use the distance between the robot and the goal as the metric.The result turns out to be unstable. As shown in the RRT search,if the first branch of the tree which comes close to the goal misses the goal by small margin,it may take relatively long time for another branch to hit the goal. So we should design another metric for this problem. Borrowing the sense of optimation, time is considered as the major factor in designing the metrics for RRT.
Intuitively, if the velocity is pointing toward the target(the goal or a randomly selected point),it will cost less time to reach the target than if there exists an angle between the velocity and the line of sight . Qualitively,it can be assumed that the large the angle is,the longer it will take to reach the target area. Thus we designed a special metric which has been proven to work well for this hitting problem.
L = S * (a * a + 1)
where L is the metric, S is the distance, a is the angle between the velocity direction and the line of sight in radian.
Quantitively, 40 degrees of this angle equals to twice the distance in the sence that it will take equal time for the robot to hit the target in both cases.
RRT growing model
Biased RRT growing model is used. 5% of the states generated by thr random state generator is the goal.
The random path generated using this metric is shown. Also the RRT searching process is recorded.Hitting time is 36.3 seconds. It about 15% more then the optimal solution.
For the Rendezvous problem,the velocity of robot is wanted to be the predetermined value when the robot reaches the goal. This task is not as easy as it looks like because we cannot turn off the pushing force. FFSQP failed(or not enough human interfering has been done in order to get a solution) to solve this problem in the present of the 4 circular obstacles. Thus we remove all obstacles from the world and then used FFSQP to get the solution for zero terminal speed Rendezvous. 1498 whole path integration iterations were done by FFSQP.The tereminal time is 0.298. The optimal rendvzvous is shown.
RRT based solution
First we design the metric as the 2nd norm defined in the the 4 dimensional vector space. Weighting is put on the velocity part. But the result turned to be unsatisfatory or no solution can be obtained even for reaching the goal region which is defined as a 4 dimensional sphere of radius 5. Referring to the optimal rendezvous trajectory, we can find that the optimal control ignores the purpose of Rendezvous for the majority of the path range. First it drives the robot toward the goal as fast as possible,then in the vicinity of the goal, the robot is steered to reduce its velocity.Based on this observance,we may design the metric by combining the effect of distance,velocity and angle between the velocity and the line of sight. Obviously,these 3 factors determine how soon the robot can rendevzvous at the target. Based on this configuring, a variable weighting factor for the velocity is design. Then the same metric scheme used for hitting problem is used to get the overall metric.
RRT growing model
Gradually biased RRT growing model is used. 5% of the states generated by thr random state generator is the goal.25% of the states generated is located in the vicinity of the goal within a location distance of 7.
Three different terminal velocity settings are computed to test this metric.When the Rendezvous velocity is relaxed to some relatively larger values the circular obstacles are put in the world.The goal region is defined to be a ball with radius 1 in terms of the metric.
case 1.
Vx = Vy = 0.
5813 nodes are explored in the RRT search. The path contains 305 nodes,or equivalentally 46 seconds.
case 2.
Vx = 1.5, Vy = 0.
7510 nodes are explored in the RRT search. The path contains 251 nodes, or equivalentally 38 seconds.
case 3.
Vx = 3.5, Vy = 1.
The obstacles sre place in the world.4856 nodes are explored in the RRT search search. The path contains 221 nodes, or equivalentally 33 seconds.
1. To design a good metric, we must get better understanding of the underlying physical characteristics of the dynamic system.
2. The metric doesn't necessarily need to obey the standard metric definition. But it should be meaningful in terms of representing certain physical index like shortest time, etc.
3. Further effort may be made to apply some optimal control algorithm in designing the metric.
4. If for every pair of the current robot state and the randomly generated state, we can solve the analytic optimal path or control law, then the problem is reduced to a pure optimal control problem. Unfortunately,this is impossible for most nonlinesr system. Thus The essence of using RRT is to design quasi-optimal metric. If that metric can lead the direction of the control close to the one from optimal control law, the RRT base method will be the ideal method to solve those problem.
1. LaValle,S.,ComS576 Lecture Notes, Spring 2000.
2. Zhou,J.L.,Tits,A.L., and Lawrence,C.T.,"User's Guide for FFSQP Version 3.7: A Fortran Code for Solving Constrained Nonlinear(Minimax) Optimization Problems,Generating Iterates Satisfying all Inequality and Linear Constraints,"Sytems Research Center,TR-92-107r2,University of Maryland,College Park,MD,April 1997.
3. Lu,P., Hanson,J.M.,"Entry Guidance for the X-33 Vehicle" Journal of Spacecraft and Rockets,Volume 35,Number 3,Page342-349.
4. Lewis,F.L., Syrmos,V.L.,"Optimal Control" John Wiley & Sons,Inc.,1995.