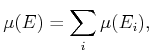5.1.3 Basic Measure Theory Definitions
This section briefly indicates how to define volume in a metric space.
This provides a basis for defining concepts such as integrals or
probability densities. Measure theory is an advanced mathematical
topic that is well beyond the scope of this book; however, it is
worthwhile to briefly introduce some of the basic definitions because
they sometimes arise in sampling-based planning.
Measure can be considered as a function that produces real values for
subsets of a metric space, 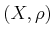 . Ideally, we would like to
produce a nonnegative value,
. Ideally, we would like to
produce a nonnegative value,
![$ \mu(A) \in [0,\infty]$](img1730.gif) , for any subset
, for any subset
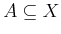 . Unfortunately, due to the Banach-Tarski paradox, if
. Unfortunately, due to the Banach-Tarski paradox, if
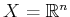 , there are some subsets for which trying to assign volume
leads to a contradiction. If
, there are some subsets for which trying to assign volume
leads to a contradiction. If 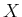 is finite, this cannot happen.
Therefore, it is hard to visualize the problem; see [836] for a
construction of the bizarre nonmeasurable sets. Due to this
problem, a workaround was developed by defining a collection of
subsets that avoids the paradoxical sets. A collection
is finite, this cannot happen.
Therefore, it is hard to visualize the problem; see [836] for a
construction of the bizarre nonmeasurable sets. Due to this
problem, a workaround was developed by defining a collection of
subsets that avoids the paradoxical sets. A collection 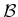 of
subsets of
of
subsets of 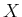 is called a sigma algebra if the following axioms
are satisfied:
is called a sigma algebra if the following axioms
are satisfied:
- The empty set is in
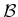 .
.
- If
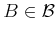 , then
, then
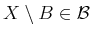 .
.
- For any collection of a countable number of sets in
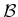 , their
union must also be in
, their
union must also be in 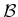 .
.
Note that the last two conditions together imply that the intersection
of a countable number of sets in 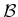 is also in
is also in 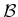 . The sets in
. The sets in
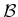 are called the measurable sets.
are called the measurable sets.
A nice sigma algebra, called the Borel sets, can be formed from
any metric space 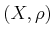 as follows. Start with the set of all
open balls in
as follows. Start with the set of all
open balls in 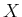 . These are the sets of the form
. These are the sets of the form
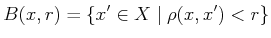 |
(5.13) |
for any 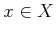 and any
and any
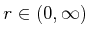 . From the open balls,
the Borel sets
. From the open balls,
the Borel sets 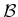 are the sets that can be constructed from
these open balls by using the sigma algebra axioms. For example, an
open square in
are the sets that can be constructed from
these open balls by using the sigma algebra axioms. For example, an
open square in
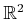 is in
is in 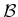 because it can be constructed as the
union of a countable number of balls (infinitely many are needed
because the curved balls must converge to covering the straight square
edges). By using Borel sets, the nastiness of nonmeasurable sets is
safely avoided.
because it can be constructed as the
union of a countable number of balls (infinitely many are needed
because the curved balls must converge to covering the straight square
edges). By using Borel sets, the nastiness of nonmeasurable sets is
safely avoided.
Example 5..9 (Borel Sets)
A simple example of
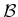
can be constructed for
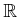
. The open balls
are just the set of all open intervals,
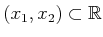
, for
any
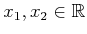
such that
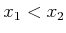
.

Using 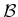 , a measure
, a measure 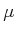 is now defined as a function
is now defined as a function
![$ \mu:
{\cal B}\rightarrow [0,\infty]$](img1741.gif) such that the measure axioms are
satisfied:
such that the measure axioms are
satisfied:
- For the empty set,
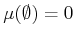 .
.
- For any collection,
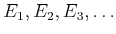 , of a countable
(possibly finite) number of pairwise disjoint, measurable sets, let
, of a countable
(possibly finite) number of pairwise disjoint, measurable sets, let
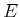 denote their union. The measure
denote their union. The measure 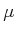 must satisfy
must satisfy
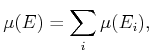 |
(5.14) |
in which 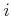 counts over the whole collection.
counts over the whole collection.
Example 5..10 (Lebesgue Measure)
The most common and important measure is the
Lebesgue measure,
which becomes the standard notions of length in
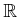
, area in
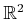
, and volume in
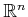
for
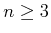
. One important concept
with Lebesgue measure is the existence of sets of
measure zero.
For any countable set
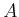
, the Lebesgue measure yields
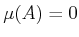
.
For example, what is the total length of the point
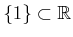
? The length of any single point must be zero. To satisfy the
measure axioms, sets such as
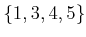
must also have measure
zero. Even infinite subsets such as
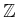
and
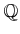
have measure zero
in
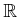
. If the dimension of a set
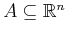
is
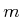
for
some integer
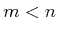
, then
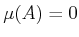
, according to the Lebesgue
measure on
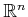
. For example, the set
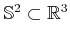
has
measure zero because the sphere has no volume. However, if the
measure space is restricted to
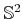
and then the surface area is
defined, then nonzero measure is obtained.

Example 5..11 (The Counting Measure)
If
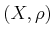
is finite, then the
counting measure can be
defined. In this case, the measure can be defined over the entire
power set of
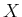
. For any
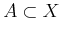
, the counting measure yields
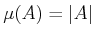
, the number of elements in
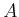
. Verify that this
satisfies the measure axioms.

Example 5..12 (Probability Measure)
Measure theory even unifies discrete and continuous probability
theory. The measure
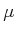
can be defined to yield probability mass.
The probability axioms (see Section
9.1.2) are
consistent with the measure axioms, which therefore yield a measure
space. The integrals and sums needed to define expectations of random
variables for continuous and discrete cases, respectively, unify into
a single measure-theoretic integral.

Measure theory can be used to define very general notions of
integration that are much more powerful than the Riemann integral that
is learned in classical calculus. One of the most important concepts
is the Lebesgue integral. Instead of being limited to
partitioning the domain of integration into intervals, virtually any
partition into measurable sets can be used. Its definition requires
the notion of a measurable function to ensure that the function
domain is partitioned into measurable sets. For further study, see
[346,546,836].
Steven M LaValle
2012-04-20

![]() . Ideally, we would like to
produce a nonnegative value,
. Ideally, we would like to
produce a nonnegative value,
![]() , for any subset
, for any subset
![]() . Unfortunately, due to the Banach-Tarski paradox, if
. Unfortunately, due to the Banach-Tarski paradox, if
![]() , there are some subsets for which trying to assign volume
leads to a contradiction. If
, there are some subsets for which trying to assign volume
leads to a contradiction. If ![]() is finite, this cannot happen.
Therefore, it is hard to visualize the problem; see [836] for a
construction of the bizarre nonmeasurable sets. Due to this
problem, a workaround was developed by defining a collection of
subsets that avoids the paradoxical sets. A collection
is finite, this cannot happen.
Therefore, it is hard to visualize the problem; see [836] for a
construction of the bizarre nonmeasurable sets. Due to this
problem, a workaround was developed by defining a collection of
subsets that avoids the paradoxical sets. A collection ![]() of
subsets of
of
subsets of ![]() is called a sigma algebra if the following axioms
are satisfied:
is called a sigma algebra if the following axioms
are satisfied:
![]() as follows. Start with the set of all
open balls in
as follows. Start with the set of all
open balls in ![]() . These are the sets of the form
. These are the sets of the form
![]() , a measure
, a measure ![]() is now defined as a function
is now defined as a function
![]() such that the measure axioms are
satisfied:
such that the measure axioms are
satisfied: