7.1.1 Problem Formulation
The formulation is designed to allow the tools and concepts learned so
far to be applied directly. Let
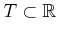 denote the time
interval, which may be bounded or unbounded. If
denote the time
interval, which may be bounded or unbounded. If 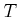 is
bounded, then
is
bounded, then
![$ T = [0,t_f]$](img2519.gif) , in which 0 is the initial time
and
, in which 0 is the initial time
and 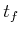 is the final time. If
is the final time. If 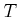 is unbounded, then
is unbounded, then
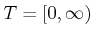 . An initial time other than 0 could alternatively be
defined without difficulty, but this will not be done here.
. An initial time other than 0 could alternatively be
defined without difficulty, but this will not be done here.
Let the state space 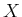 be defined as
be defined as
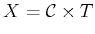 , in which
, in which
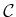 is the usual C-space of the robot, as defined in Chapter
4. A state
is the usual C-space of the robot, as defined in Chapter
4. A state 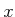 is represented as
is represented as 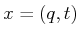 , to
indicate the configuration
, to
indicate the configuration 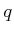 and time
and time 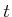 components of the
state vector. The planning will occur directly in
components of the
state vector. The planning will occur directly in 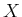 , and in many
ways it can be treated as any C-space seen to far, but there is one
critical difference: Time marches forward. Imagine a path that
travels through
, and in many
ways it can be treated as any C-space seen to far, but there is one
critical difference: Time marches forward. Imagine a path that
travels through 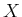 . If it first reaches a state
. If it first reaches a state 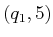 , and then
later some state
, and then
later some state 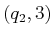 , some traveling backward through time is
required! There is no mathematical problem with allowing such time
travel, but it is not realistic for most applications. Therefore,
paths in
, some traveling backward through time is
required! There is no mathematical problem with allowing such time
travel, but it is not realistic for most applications. Therefore,
paths in 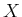 are forced to follow a constraint that they must move
forward in time.
are forced to follow a constraint that they must move
forward in time.
Now consider making the following time-varying versions of the items
used in Formulation 4.1 for motion planning.
Formulation 7..1 (The Time-Varying Motion Planning Problem)
- A world
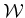 in which either
in which either
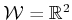 or
or
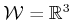 . This is the same as in Formulation 4.1.
. This is the same as in Formulation 4.1.
- A time interval
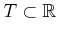 that is
either bounded to yield
that is
either bounded to yield
![$ T = [0,t_f]$](img2519.gif) for some final time,
for some final time,
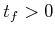 , or unbounded to yield
, or unbounded to yield
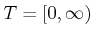 .
.
- A semi-algebraic, time-varying obstacle region
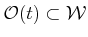 for every
for every 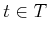 . It is assumed that the
obstacle region is a finite collection of rigid bodies that undergoes
continuous, time-dependent rigid-body transformations.
. It is assumed that the
obstacle region is a finite collection of rigid bodies that undergoes
continuous, time-dependent rigid-body transformations.
- The robot
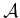 (or
(or
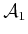 ,
,  ,
,
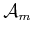 for a
linkage) and configuration space
for a
linkage) and configuration space 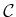 definitions are the
same as in Formulation 4.1.
definitions are the
same as in Formulation 4.1.
- The state space
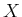 is the Cartesian product
is the Cartesian product
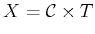 and a state
and a state 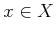 is denoted as
is denoted as 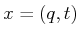 to
denote the configuration
to
denote the configuration 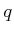 and time
and time 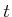 components. See Figure
7.1. The obstacle region,
components. See Figure
7.1. The obstacle region, 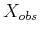 , in the state space
is defined as
, in the state space
is defined as
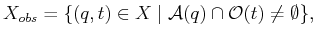 |
(7.1) |
and
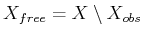 . For a given
. For a given 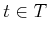 , slices of
, slices of
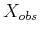 and
and
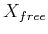 are obtained. These are denoted as
are obtained. These are denoted as
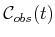 and
and
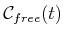 , respectively, in which (assuming
, respectively, in which (assuming 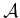 is one body)
is one body)
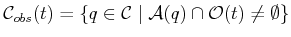 |
(7.2) |
and
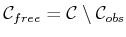 .
.
- A state
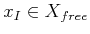 is designated as the initial
state, with the constraint that
is designated as the initial
state, with the constraint that
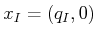 for some
for some
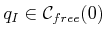 . In other words, at the initial time the robot
cannot be in collision.
. In other words, at the initial time the robot
cannot be in collision.
- A subset
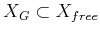 is designated as the goal
region. A typical definition is to pick some
is designated as the goal
region. A typical definition is to pick some
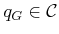 and
let
and
let
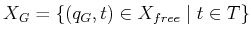 , which means
that the goal is stationary for all time.
, which means
that the goal is stationary for all time.
- A complete algorithm must compute a continuous, time-monotonic
path,
![$ \tau[0,1] \rightarrow {X_{free}}$](img2541.gif) , such that
, such that
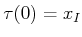 and
and
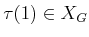 , or correctly report that such a path
does not exist. To be time-monotonic
implies that for any
, or correctly report that such a path
does not exist. To be time-monotonic
implies that for any
![$ s_1,s_2 \in [0,1]$](img2544.gif) such that
such that 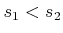 , we
have
, we
have 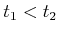 , in which
, in which
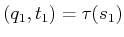 and
and
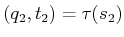 .
.
Figure 7.1:
A time-varying example with
piecewise-linear obstacle motion.
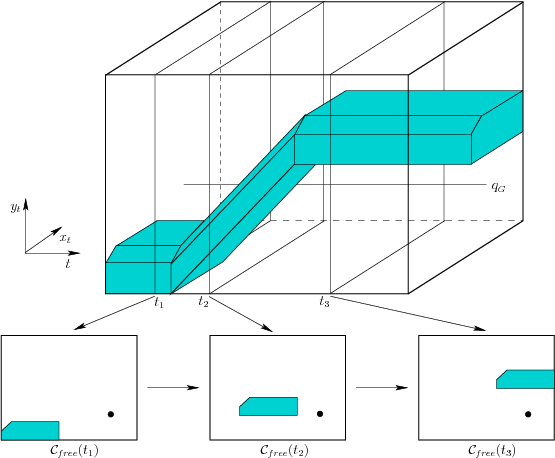 |
Example 7..1 (Piecewise-Linear Obstacle Motion)
Figure
7.1
shows an example of a convex, polygonal robot
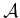
that translates
in
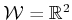
. There is a single, convex, polygonal obstacle
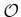
.
The two of these together yield a convex, polygonal C-space obstacle,
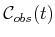
, which is shown for times
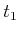
,
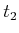
, and
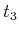
. The
obstacle moves with a
piecewise-linear motion model, which means
that transformations applied to
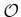
are a piecewise-linear function
of time. For example, let
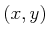
be a fixed point on the obstacle.
To be a linear motion model, this point must transform as
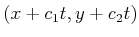
for some constants
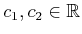
. To be
piecewise-linear, it may change to a different linear motion at a
finite number of critical times. Between these critical times, the
motion must remain linear. There are two critical times in the
example. If
is polygonal, and a piecewise-linear motion
model is used, then
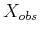
is polyhedral, as depicted in Figure
7.1. A stationary goal is also shown, which appears
as a line that is parallel to the
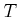
-axis.

In the general formulation, there are no additional constraints on the
path, 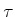 , which means that the robot motion model allows infinite
acceleration and unbounded speed. The robot velocity may change
instantaneously, but the path through
, which means that the robot motion model allows infinite
acceleration and unbounded speed. The robot velocity may change
instantaneously, but the path through 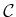 must always be continuous.
These issues did not arise in Chapter 4 because there
was no need to mention time. Now it becomes necessary.7.1
must always be continuous.
These issues did not arise in Chapter 4 because there
was no need to mention time. Now it becomes necessary.7.1
Steven M LaValle
2012-04-20

![]() denote the time
interval, which may be bounded or unbounded. If
denote the time
interval, which may be bounded or unbounded. If ![]() is
bounded, then
is
bounded, then
![]() , in which 0 is the initial time
and
, in which 0 is the initial time
and ![]() is the final time. If
is the final time. If ![]() is unbounded, then
is unbounded, then
![]() . An initial time other than 0 could alternatively be
defined without difficulty, but this will not be done here.
. An initial time other than 0 could alternatively be
defined without difficulty, but this will not be done here.
![]() be defined as
be defined as
![]() , in which
, in which
![]() is the usual C-space of the robot, as defined in Chapter
4. A state
is the usual C-space of the robot, as defined in Chapter
4. A state ![]() is represented as
is represented as ![]() , to
indicate the configuration
, to
indicate the configuration ![]() and time
and time ![]() components of the
state vector. The planning will occur directly in
components of the
state vector. The planning will occur directly in ![]() , and in many
ways it can be treated as any C-space seen to far, but there is one
critical difference: Time marches forward. Imagine a path that
travels through
, and in many
ways it can be treated as any C-space seen to far, but there is one
critical difference: Time marches forward. Imagine a path that
travels through ![]() . If it first reaches a state
. If it first reaches a state ![]() , and then
later some state
, and then
later some state ![]() , some traveling backward through time is
required! There is no mathematical problem with allowing such time
travel, but it is not realistic for most applications. Therefore,
paths in
, some traveling backward through time is
required! There is no mathematical problem with allowing such time
travel, but it is not realistic for most applications. Therefore,
paths in ![]() are forced to follow a constraint that they must move
forward in time.
are forced to follow a constraint that they must move
forward in time.
![]() , which means that the robot motion model allows infinite
acceleration and unbounded speed. The robot velocity may change
instantaneously, but the path through
, which means that the robot motion model allows infinite
acceleration and unbounded speed. The robot velocity may change
instantaneously, but the path through ![]() must always be continuous.
These issues did not arise in Chapter 4 because there
was no need to mention time. Now it becomes necessary.7.1
must always be continuous.
These issues did not arise in Chapter 4 because there
was no need to mention time. Now it becomes necessary.7.1