- Consider the obstacle region, (7.1), in the state
space for time-varying motion planning.
- To ensure that
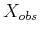 is polyhedral, what kind of paths should
be allowed? Show how the model primitives
is polyhedral, what kind of paths should
be allowed? Show how the model primitives 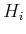 that define
that define 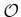 are
expressed in general, using
are
expressed in general, using 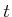 as a parameter.
as a parameter.
- Repeat the exercise, but for ensuring that
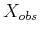 is
semi-algebraic.
is
semi-algebraic.
- Propose a way to adapt the sampling-based roadmap algorithm of
Section 5.6 to solve the problem of time-varying
motion planning with bounded speed.
- Develop an efficient algorithm for computing the obstacle region
for two translating polygonal robots that each follow a linear path.
Figure 7.43:
Two translating robots moving along
piecewise-linear paths.
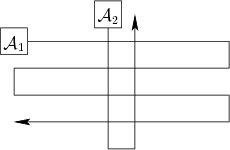 |
- Sketch the coordination space for the two robots moving along
the fixed paths shown in Figure 7.43.
- Suppose there are two robots, and each moves on its own roadmap
of three paths. The paths in each roadmap are arranged end-to-end in
a triangle.
- Characterize the fixed-roadmap coordination
space that results, including a description of its topology.
- Now suppose there are
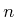 robots, each on a triangular roadmap,
and characterize the fixed-roadmap coordination space.
robots, each on a triangular roadmap,
and characterize the fixed-roadmap coordination space.
- Consider the state space obtained as the Cartesian product of
the C-spaces of
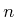 identical robots. Suppose that each robot is
labeled with a unique integer. Show that
identical robots. Suppose that each robot is
labeled with a unique integer. Show that 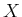 can be partitioned
nicely into
can be partitioned
nicely into 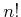 regions in which
regions in which 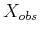 appears identical and the
only difference is the labels (which indicate the particular robots
that are in collision).
appears identical and the
only difference is the labels (which indicate the particular robots
that are in collision).
- Suppose there are two robots, and each moves on its own roadmap
of three paths. The paths in one roadmap are arranged end-to-end in a
triangle, and the paths in the other are arranged as a Y.
Characterize the fixed-roadmap coordination space that results,
including a description of its topology.
- Design an efficient algorithm that takes as input a graph
representation of the connectivity of a linkage and computes an
active-passive decomposition. Assume that all links are revolute.
The algorithm should work for either 2D or 3D linkages (the dimension
is also an input). Determine the asymptotic running time of your
algorithm.
- Consider the problem of coordinating the motion of two robots
that move along precomputed paths but in the presence of predictable
moving obstacles. Develop a planning algorithm for this problem.
- Consider a manipulator in
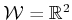 made of four links
connected in a chain by revolute joints. There is unit distance
between the joints, and the first joint is attached at
made of four links
connected in a chain by revolute joints. There is unit distance
between the joints, and the first joint is attached at 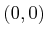 in
in
 . Suppose that the end of the last link, which is position
. Suppose that the end of the last link, which is position
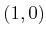 in its body frame, is held at
in its body frame, is held at
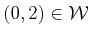 .
.
- Use kinematics expressions to express the closure constraints
for a configuration
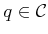 .
.
- Convert the closure constraints into polynomial form.
- Use differentiation to determine the constraints on the allowable
velocities that maintain closure at a configuration
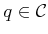 .
.
Implementations
- Implement the vertical decomposition algorithm to solve the
path-tuning problem, as shown in Figure 7.5.
- Use grid-based sampling and a search
algorithm to compute collision-free motions of three robots moving
along predetermined paths.
- Under the conditions of Exercise 12, compute
Pareto-optimal coordination strategies that optimize the time (number
of stages) that each robot takes to reach its goal. Design a
wavefront propagation algorithm that keeps track of the complete
(ignoring equivalent strategies) set of minimal Pareto-optimal
coordination strategies at each reached state. Avoid storing entire
plans at each discretized state.
- To gain an appreciation of the difficulties of planning for
closed kinematic chains, try motion planning for a point on a torus
among obstacles using only the implicit torus constraint given by
(6.40). To simplify collision detection, the obstacles
can be a collection of balls in
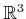 that intersect the torus.
Adapt a sampling-based planning technique, such as the bidirectional
RRT, to traverse the torus and solve
planning problems.
that intersect the torus.
Adapt a sampling-based planning technique, such as the bidirectional
RRT, to traverse the torus and solve
planning problems.
- Implement the spanning-tree coverage planning algorithm of
Section 7.6.
- Develop an RRT-based planning algorithm that
causes the robot to chase an unpredictable moving target in a planar
environment that contains obstacles. The algorithm should run quickly
enough so that replanning can occur during execution. The robot
should execute the first part of the most recently computed path while
simultaneously computing a better plan for the next time increment.
- Modify Exercise 16 so that the robot assumes the
target follows a predictable, constant-velocity trajectory until some
deviation is observed.
- Show how to handle unexpected obstacles by using a fast enough
planning algorithm. For simplicity, suppose the robot is a point
moving in a polygonal obstacle region. The robot first computes a
path and then starts to execute it. If the obstacle region changes,
then a new path is computed from the robot's current position. Use
vertical decomposition or another algorithm of your choice (provided
it is fast enough). The user should be able to interactively place or
move obstacles during plan execution.
- Use the manipulation planning framework of Section
7.3.2 to develop an algorithm that solves the famous
Towers of Hanoi problem by a robot that carries the rings
[166]. For simplicity, suppose a polygonal robot moves
polygonal parts in
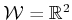 and rotation is not allowed. Make
three pegs, and initially place all parts on one peg, sorted from
largest to smallest. The goal is to move all of the parts to another
peg while preserving the sorting.
and rotation is not allowed. Make
three pegs, and initially place all parts on one peg, sorted from
largest to smallest. The goal is to move all of the parts to another
peg while preserving the sorting.
- Use grid-based approximation to solve optimal planning problems
for a point robot in the plane. Experiment with using different
neighborhoods and metrics. Characterize the combinations under which
good and bad approximations are obtained.
Steven M LaValle
2012-04-20
