
Next: 9.2 A Game Against Up: 9.1 Preliminary Concepts Previous: Expectation
Up until now, any actions taken in a plan have been deterministic. The plans in Chapter 2 specified actions with complete certainty. Formulation 9.1 was solved by specifying the best action. It can be viewed as a strategy that trivially makes the same decision every time.
In some applications, the decision maker may not want to be
predictable. To achieve this, randomization can be incorporated into
the strategy. If ![]() is discrete, a randomized strategy,
is discrete, a randomized strategy,
![]() , is specified by a probability distribution,
, is specified by a probability distribution, ![]() , over
, over
![]() . Let
. Let ![]() denote the set of all possible randomized strategies.
When the strategy is applied, an action
denote the set of all possible randomized strategies.
When the strategy is applied, an action ![]() is chosen by
sampling according to the probability distribution,
is chosen by
sampling according to the probability distribution, ![]() . We now
have to make a clear distinction between defining the strategy
and applying the strategy. So far, the two have been
equivalent; however, a randomized strategy must be executed to
determine the resulting action. If the strategy is executed
repeatedly, it is assumed that each trial is independent of the
actions obtained in previous trials. In other words,
. We now
have to make a clear distinction between defining the strategy
and applying the strategy. So far, the two have been
equivalent; however, a randomized strategy must be executed to
determine the resulting action. If the strategy is executed
repeatedly, it is assumed that each trial is independent of the
actions obtained in previous trials. In other words,
![]() , in which
, in which
![]() represents the probability that the
strategy chooses action
represents the probability that the
strategy chooses action ![]() in trial
in trial ![]() , given that
, given that ![]() was
chosen in trial
was
chosen in trial ![]() for some
for some ![]() . If
. If ![]() is continuous, then a
randomized strategy may be specified by a probability density
function,
is continuous, then a
randomized strategy may be specified by a probability density
function, ![]() . In decision-theory and game-theory literature,
deterministic and randomized strategies are often referred to as pure and mixed, respectively.
. In decision-theory and game-theory literature,
deterministic and randomized strategies are often referred to as pure and mixed, respectively.
A deterministic strategy can always be viewed as a special case of a
randomized strategy, if you are not bothered by events that have
probability zero. A deterministic strategy, ![]() , can be
simulated by a random strategy by assigning
, can be
simulated by a random strategy by assigning ![]() if
if ![]() ,
and
,
and ![]() otherwise. Only with probability zero can different
actions be chosen (possible, but not probable!).
otherwise. Only with probability zero can different
actions be chosen (possible, but not probable!).
Imagine using a randomized strategy to solve a problem expressed using
Formulation 9.1. The first difficulty appears to be
that the cost cannot be predicted. If the strategy is applied
numerous times, then we can define the average cost. As the number of
times tends to infinity, this average would converge to the expected
cost, denoted by
![]() , if
, if ![]() is treated as a random
variable (in addition to the cost function). If
is treated as a random
variable (in addition to the cost function). If ![]() is discrete, the
expected cost of a randomized strategy
is discrete, the
expected cost of a randomized strategy ![]() is
is
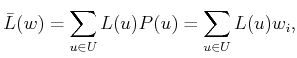 |
(9.13) |
An interesting question is whether there exists some ![]() such that
such that
![]() , for all
, for all ![]() . In other words,
do there exist randomized strategies that are better than all
deterministic strategies, using Formulation 9.1? The
answer is no because the best strategy is always to assign
probability one to the action,
. In other words,
do there exist randomized strategies that are better than all
deterministic strategies, using Formulation 9.1? The
answer is no because the best strategy is always to assign
probability one to the action, ![]() , that minimizes
, that minimizes ![]() . This is
equivalent to using a deterministic strategy. If there are two or
more actions that obtain the optimal cost, then a randomized strategy
could arbitrarily distribute all of the probability mass between
these. However, there would be no further reduction in cost.
Therefore, randomization seems pointless in this context, unless there
are other considerations.
. This is
equivalent to using a deterministic strategy. If there are two or
more actions that obtain the optimal cost, then a randomized strategy
could arbitrarily distribute all of the probability mass between
these. However, there would be no further reduction in cost.
Therefore, randomization seems pointless in this context, unless there
are other considerations.
One important example in which a randomized strategy is of critical importance is when making decisions in competition with an intelligent adversary. If the problem is repeated many times, an opponent could easily learn any deterministic strategy. Randomization can be used to weaken the prediction capabilities of an opponent. This idea will be used in Section 9.3 to obtain better ways to play zero-sum games.
Following is an example that illustrates the advantage of randomization when repeatedly playing against an intelligent opponent.
A generalization of this to three actions is the famous game of
Rock-Paper-Scissors [958]. If you want to design a computer
program that repeatedly plays this game against smart opponents, it
seems best to incorporate randomization.
![]()
Steven M LaValle 2012-04-20