
Next: 9.4.1.1 Dealing with multiple Up: 9.4 Nonzero-Sum Games Previous: 9.4 Nonzero-Sum Games
To help make the connection to Section 9.3 smoother, two-player games will be considered first. This case is also easier to understand because the notation is simpler. The ideas are then extended without difficulty from two players to many players. The game is formulated as follows.
Paralleling Section 9.3, first consider applying deterministic strategies to solve the game. As before, one possibility is that a player can apply its security strategy. To accomplish this, it does not even need to look at the cost function of the other player. It seems somewhat inappropriate, however, to neglect the consideration of both cost functions when making a decision. In most cases, the security strategy results in regret, which makes it inappropriate for nonzero-sum games.
A strategy that avoids regret will now be given. A pair
![]() of actions is defined to be a Nash equilibrium
if
of actions is defined to be a Nash equilibrium
if
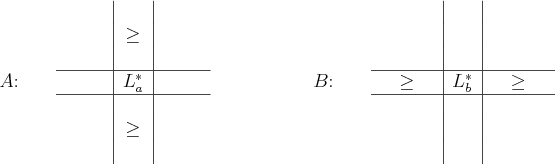 |
The game in Formulation 9.8 can be completely
represented using two cost matrices. Let ![]() and
and ![]() denote the cost
matrices for
denote the cost
matrices for
![]() and
and
![]() , respectively. Recall that Figure
9.2 showed a pattern for detecting a saddle point. A
Nash equilibrium can be detected as shown in Figure
9.5. Think about the relationship between the two.
If
, respectively. Recall that Figure
9.2 showed a pattern for detecting a saddle point. A
Nash equilibrium can be detected as shown in Figure
9.5. Think about the relationship between the two.
If ![]() , then
, then ![]() can be negated and superimposed on top of
can be negated and superimposed on top of ![]() .
This will yield the pattern in Figure 9.2 (each
.
This will yield the pattern in Figure 9.2 (each
![]() becomes
becomes ![]() because of negation). The values
because of negation). The values ![]() and
and
![]() coincide in this case. This observation implies that if
coincide in this case. This observation implies that if ![]() , then the Nash equilibrium is actually the same concept as a
saddle point. It applies, however, to much more general games.
, then the Nash equilibrium is actually the same concept as a
saddle point. It applies, however, to much more general games.
For zero-sum games, the existence of multiple saddle points did not
cause any problem; however, for nonzero-sum games, there are great
troubles. In the example shown here, one Nash equilibrium is clearly
better than the other for both players. Therefore, it may seem
reasonable that a rational DM would choose the better one. The issue
of multiple Nash equilibria will be discussed next.
![]()