11.2.2 Nondeterministic Information Spaces

This section defines the I-map ${{\kappa}_{ndet}}$ from Figure 11.3, which converts each history I-state into a subset of $X$ that corresponds to all possible current states. Nature is modeled nondeterministically, which means that there is no information about what actions nature will choose, other than that they will be chosen from $\Theta$ and $\Psi$. Assume that the state-action sensor mapping from Section 11.1.1 is used. Consider what inferences may be drawn from a history I-state, ${\eta}_k = ({\eta_0},{\tilde{u}}_{k-1},{\tilde{y}}_k)$. Since the model does not involve probabilities, let ${\eta_0}$ represent a set $X_1 \subseteq X$. Let ${{\kappa}_{ndet}}({\eta}_k)$ be the minimal subset of $X$ in which $x_k$ is known to lie given ${\eta}_k$. This subset is referred to as a nondeterministic I-state. To remind you that ${{\kappa}_{ndet}}({\eta}_k)$ is a subset of $X$, it will now be denoted as $X_k({\eta}_k)$. It is important that $X_k({\eta}_k)$ be as small as possible while consistent with ${\eta}_k$.

Recall from (11.6) that for every observation $y_k$, a set $H(y_k) \subseteq X$ of possible values for $x_k$ can be inferred. This could serve as a crude estimate of the nondeterministic I-state. It is certainly known that $X_k({\eta}_k) \subseteq H(y_k)$; otherwise, $x_k$, would not be consistent with the current sensor observation. If we carefully progress from the initial conditions while applying constraints due to the state transition equation, the appropriate subset of $H(y_k)$ will be obtained.

From the state transition function $f$, define a set-valued function $F$ that yields a subset of $X$ for every $x \in X$ and $u \in U$ as

$$F(x,u) = \{ x^\prime \in X \;\vert\; \mbox{ $\exists \theta \in \Theta(x,u)$ for which } x^\prime = f(x,u,\theta) \} .$$ (11.28)

Note that both $F$ and $H$ are set-valued functions that eliminate the direct appearance of nature actions. The effect of nature is taken into account in the set that is obtained when these functions are applied. This will be very convenient for computing the nondeterministic I-state.

An inductive process will now be described that results in computing the nondeterministic I-state, $X_k({\eta}_k)$, for any stage $k$. The base case, $k=1$, of the induction proceeds as

$$X_1({\eta}_1) = X_1({\eta_0},y_1) = X_1 \cap H(y_1) .$$ (11.29)

The first part of the equation replaces ${\eta}_1$ with $({\eta_0},y_1)$, which is a longer way to write the history I-state. There are not yet any actions in the history. The second part applies set intersection to make consistent the two pieces of information: 1) The initial state lies in $X_1$, which is the initial condition, and 2) the states in $H(y_1)$ are possible given the observation $y_1$.

Now assume inductively that $X_k({\eta}_k) \subseteq X$ has been computed and the task is to compute $X_{k+1}({\eta}_{k+1})$. From (11.15), ${\eta}_{k+1} = ({\eta}_k,u_k,y_{k+1})$. Thus, the only new pieces of information are that $u_k$ was applied and $y_{k+1}$ was observed. These will be considered one at a time.

Consider computing $X_{k+1}({\eta}_k,u_k)$. If $x_k$ was known, then after applying $u_k$, the state could lie anywhere within $F(x_k,u_k)$, using (11.28). Although $x_k$ is actually not known, it is at least known that $x_k \in X_k({\eta }_k)$. Therefore,

$$X_{k+1}({\eta}_k,u_k) = \bigcup_{x_k \in X_k({\eta}_k)} F(x_k,u_k) .$$ (11.30)

This can be considered as the set of all states that can be reached by starting from some state in $X_k({\eta}_k)$ and applying any actions $u_k \in U$ and $\theta_k \in \Theta(x_k,u_k)$. See Figure 11.5.

Figure 11.5: The first step in computing the nondeterministic I-state is to take the union of $F(x_k,u_k)$ over all possible $x_k \in X_k({\eta }_k)$.

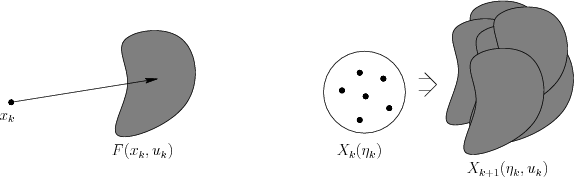The next step is to take into account the observation $y_{k+1}$. This information alone indicates that $x_{k+1}$ lies in $H(y_{k+1})$. Therefore, an intersection is performed to obtain the nondeterministic I-state,

$$X_{k+1}({\eta}_{k+1}) = X_{k+1}({\eta}_k,u_k,y_{k+1}) = X_{k+1}({\eta}_k,u_k) \cap H(y_{k+1}) .$$ (11.31)

Thus, it has been shown how to compute $X_{k+1}({\eta}_{k+1})$ from $X_k({\eta}_k)$. After starting with (11.29), the nondeterministic I-states at any stage can be computed by iterating (11.30) and (11.31) as many times as necessary.

Since the nondeterministic I-state is always a subset of $X$, the nondeterministic I-space, ${\cal I}_{ndet}= {\rm pow}(X)$, is obtained (shown in Figure 11.3). If $X$ is finite, then ${\cal I}_{ndet}$ is also finite, which was not the case with ${\cal I}_{hist}$ because the histories continued to grow with the number of stages. Thus, if the number of stages is unbounded or large in comparison to the size of $X$, then nondeterministic I-states seem preferable. It is also convenient that ${{\kappa}_{ndet}}$ is a sufficient I-map, as defined in Section 11.2.1. This implies that a planning problem can be completely expressed in terms of ${\cal I}_{ndet}$ without maintaining the histories. The goal region, $X_G$, can be expressed directly as a nondeterministic I-state. In this way, the planning task is to terminate in a nondeterministic I-state, $X_k({\eta}_k)$, for which $X_k({\eta}_k) \subseteq X_G$.

The sufficiency of ${{\kappa}_{ndet}}$ is obtained because (11.30) and (11.31) show that $X_{k+1}({\eta}_{k+1})$ can be computed from $X_k({\eta}_k)$, $u_k$, and $y_{k+1}$. This implies that a derived information transition equation can be formed. The nondeterministic I-space can also be treated as ``just another state space.'' Although many history I-states may map to the same nondeterministic I-state, it has been assumed for decision-making purposes that particular history is irrelevant, once $X_k({\eta}_k)$ is given.

The following example is not very interesting in itself, but it is simple enough to illustrate the concepts.

Example 11..13 (Three-State Example)   Let $X = \{0,1,2\}$, $U = \{-1,0,1\}$, and $\Theta(x,u) = \{0,1\}$ for all $x \in X$ and $u \in U$. The state transitions are given by $f(x,u,\theta) = (x + u + \theta) \mod 3$. Regarding sensing, $Y = \{0,1,2,3,4\}$ and $\Psi(x) = \{0,1,2\}$ for all $x \in X$. The sensor mapping is $y = h(x,\psi) = x + \psi$.

The history I-space appears very cumbersome for this example, which only involves three states. The nondeterministic I-space for this example is

$${\cal I}_{ndet}= \{\emptyset,\{0\},\{1\},\{2\},\{0,1\},\{1,2\},\{0,2\},\{0,1,2\}\} ,$$ (11.32)

which is the power set of $X = \{0,1,2\}$. Note, however, that the empty set, $\emptyset$, can usually be deleted from ${\cal I}_{ndet}$.^11.3 Suppose that the initial condition is $X_1 = \{0,2\}$ and that the initial state is $x_1 = 0$. The initial state is unknown to the decision maker, but it is needed to ensure that valid observations are made in the example.

Now consider the execution over a number of stages. Suppose that the first observation is $y_1 = 2$. Based on the sensor mapping, $H(y_1) = H(2) = \{0,1,2\}$, which is not very helpful because $H(2) = X$. Applying (11.29) yields $X_1({\eta}_1) = \{0,2\}$. Now suppose that the decision maker applies the action $u_1 = 1$ and nature applies $\theta_1 = 1$. Using $f$, this yields $x_2 = 2$. The decision maker does not know $\theta_1$ and must therefore take into account any nature action that could have been applied. It uses (11.30) to infer that

$$X_2({\eta}_1,u_1) = F(2,1) \cup F(0,1) = \{0,1\} \cup \{1,2\} = \{0,1,2\} .$$ (11.33)

Now suppose that $y_2 = 3$. From the sensor mapping, $H(3) = \{1,2\}$. Applying (11.31) yields

$$X_2({\eta}_2) = X_2({\eta}_1,u_1) \cap H(y_2) = \{0,1,2\} \cap \{1,2\} = \{1,2\} .$$ (11.34)

This process may be repeated for as many stages as desired. A path is generated through ${\cal I}_{ndet}$ by visiting a sequence of nondeterministic I-states. If the observation $y_k = 4$ is ever received, the state, $x_k$, becomes immediately known because $H(4) = \{2\}$. $\blacksquare$