One problem that typically arises in mobile robotics is that optimal
motion plans bring robots too close to obstacles. Recall from Section
6.2.4 that the shortest Euclidean paths for motion
planning in a polygonal environment must be allowed to touch obstacle
vertices. This motivated the maximum clearance roadmap, which was
covered in Section 6.2.3. A grid-based approximate
version of the maximum clearance roadmap can be made. Furthermore, a
navigation function can be defined that guides the robot onto the
roadmap, then travels along the roadmap, and finally deposits the
robot at a specified goal. In [588], the resulting navigation
function is called NF2.
Assume that there is a single goal state,
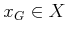 . The
computation of a maximum clearance navigation function proceeds as
follows:
. The
computation of a maximum clearance navigation function proceeds as
follows:
- Instead of
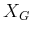 , assign
, assign 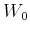 to be the set of all states
from which motion in at least one direction is blocked. These are the
states on the boundary of the discretized collision-free space.
to be the set of all states
from which motion in at least one direction is blocked. These are the
states on the boundary of the discretized collision-free space.
- Perform wavefront iterations that propagate costs in waves
outward from the obstacle boundaries.
- As the wavefronts propagate, they will meet approximately at the
location of the maximum clearance roadmap for the original, continuous
problem. Mark any state at which two wavefront points arrive from
opposing directions as a skeleton state. It may be the case
that the wavefronts simply touch each other, rather than arriving at a
common state; in this case, one of the two touching states is chosen
as the skeleton state. Let
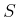 denote the set of all skeleton states.
denote the set of all skeleton states.
- After the wavefront propagation ends, connect
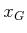 to the
skeleton by inserting
to the
skeleton by inserting 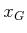 and all states along the path to the
skeleton into
and all states along the path to the
skeleton into 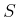 . This path can be found using any search algorithm.
. This path can be found using any search algorithm.
- Compute a navigation function
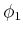 over
over 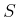 by treating
all other states as if they were obstacles and using the wavefront
propagation algorithm. This navigation function guides any point in
by treating
all other states as if they were obstacles and using the wavefront
propagation algorithm. This navigation function guides any point in
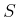 to the goal.
to the goal.
- Treat
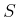 as a goal region and compute a navigation function
as a goal region and compute a navigation function
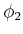 using the wavefront propagation algorithm. This navigation
function guides the state to the nearest point on the skeleton.
using the wavefront propagation algorithm. This navigation
function guides the state to the nearest point on the skeleton.
- Combine
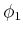 and
and 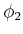 as follows to obtain
as follows to obtain 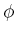 . For
every
. For
every 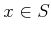 , let
, let
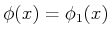 . For every remaining
state, the value
. For every remaining
state, the value
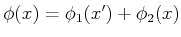 is assigned, in
which
is assigned, in
which 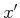 is the nearest state to
is the nearest state to  such that
such that 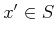 . The
state
. The
state 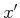 can easily be recorded while
can easily be recorded while 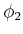 is computed.
is computed.
If
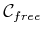 is multiply connected, then there may be multiple ways to
each
is multiply connected, then there may be multiple ways to
each 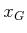 by traveling around different obstacles (the paths are
not homotopic). The method described above does not take into account
the problem that one route may have a tighter clearance than another.
The given approach only optimizes the distance traveled along the
skeleton; it does not, however, maximize the nearest approach to an
obstacle, if there are multiple routes.
by traveling around different obstacles (the paths are
not homotopic). The method described above does not take into account
the problem that one route may have a tighter clearance than another.
The given approach only optimizes the distance traveled along the
skeleton; it does not, however, maximize the nearest approach to an
obstacle, if there are multiple routes.
Steven M LaValle
2012-04-20

![]() . The
computation of a maximum clearance navigation function proceeds as
follows:
. The
computation of a maximum clearance navigation function proceeds as
follows: