
Next: Odometry sensors Up: 11.5.1 Sensor Models Previous: Landmark sensors
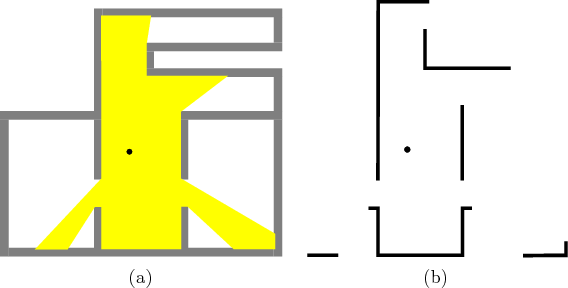
In many robotics applications, the robot may not have a map of the obstacles in the world. In this case, sensing is used to both learn the environment and to determine its position and orientation within the environment. Suppose that a robot is dropped into an environment as shown in Figure 11.14a. For problems such as this, the state represents both the position of the robot and the obstacles themselves. This situation is explained in further detail in Section 12.3. Here, some sensor models for problems of this type are given. These are related to the boundary and proximity sensors of Figure 11.12, but they yield more information when the robot is not at the boundary.
One of the oldest sensors used in mobile robotics is an acoustic sonar, which emits a high-frequency sound wave in a specific
direction and measures the time that it takes for the wave to reflect
off a wall and return to the sonar (often the sonar serves as both a
speaker and a microphone). Based on the speed of sound and the time
of flight, the distance to the wall can be estimated. Sometimes, the
wave never returns; this can be modeled with nature. Also, errors in
the distance estimate can be modeled with nature. In general, the
observation space ![]() for a single sonar is
for a single sonar is
![]() , in which
, in which
![]() indicates that the wave did not return. The interpretation
of
indicates that the wave did not return. The interpretation
of ![]() could be the time of flight, or it could already be transformed
into estimated distance. If there are
could be the time of flight, or it could already be transformed
into estimated distance. If there are ![]() sonars, each pointing in a
different direction, then
sonars, each pointing in a
different direction, then
![]() , which indicates that one
reading can be obtained for each sonar. For example, Figure
11.14b shows four sonars and the distances that they can
measure. Each observation therefore yields a point in
, which indicates that one
reading can be obtained for each sonar. For example, Figure
11.14b shows four sonars and the distances that they can
measure. Each observation therefore yields a point in
![]() .
.
 |
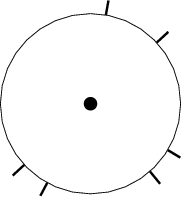
Modern laser scanning technology enables very accurate distance
measurements with very high angular density. For example, the
SICK LMS-200 can obtain a distance measurement for at least
every 1/2 degree and sweep the full 360 degrees at least 30 times a
second. The measurement accuracy in an indoor environment is often on
the order of a few millimeters. Imagine the limiting case, which is
like having a continuum of sonars, one for every angle in
![]() .
This results in a sensor called a range scanner or
visibility sensor, which provides a distance measurement for
each
.
This results in a sensor called a range scanner or
visibility sensor, which provides a distance measurement for
each
![]() , as shown in Figure 11.15.
, as shown in Figure 11.15.
 |
A weaker sensor can be made by only indicating points in
![]() at
which discontinuities (or gaps) occur in the depth scan. Refer to
this as a gap sensor; an example is shown in Figure
11.16. It might even be the case that only the circular
ordering of these gaps is given around
at
which discontinuities (or gaps) occur in the depth scan. Refer to
this as a gap sensor; an example is shown in Figure
11.16. It might even be the case that only the circular
ordering of these gaps is given around
![]() , without knowing the
relative angles between them, or the distance to each gap. A planner
based on this sensing model is presented in Section 12.3.4.
, without knowing the
relative angles between them, or the distance to each gap. A planner
based on this sensing model is presented in Section 12.3.4.
Steven M LaValle 2012-04-20