
Next: 13.2.3 Nonlinear Systems Up: 13.2 Phase Space Representation Previous: 13.2.1.3 Higher order differential
Now that the phase space has been defined as a special kind of state space that can handle dynamics, it is convenient to classify the kinds of differential models that can be defined based on their mathematical form. The class of linear systems has been most widely studied, particularly in the context of control theory. The reason is that many powerful techniques from linear algebra can be applied to yield good control laws [192]. The ideas can also be generalized to linear systems that involve optimality criteria [28,570], nature [95,564], or multiple players [59].
Let
![]() be a phase space, and let
be a phase space, and let
![]() be an action
space for
be an action
space for ![]() . A linear system is a differential model
for which the state transition equation can be expressed as
. A linear system is a differential model
for which the state transition equation can be expressed as
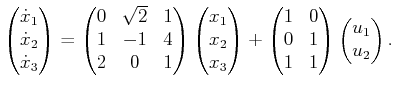 |
(13.38) |
Recall from Section 13.1.1 that ![]() linear constraints restrict the velocity to an
linear constraints restrict the velocity to an ![]() -dimensional hyperplane. The
linear model in (13.37) is in parametric form, which means
that each action variable may allow an independent degree of
freedom. In this case,
-dimensional hyperplane. The
linear model in (13.37) is in parametric form, which means
that each action variable may allow an independent degree of
freedom. In this case, ![]() . In the extreme case of
. In the extreme case of ![]() ,
there are no actions, which results in
,
there are no actions, which results in
![]() . The phase
velocity
. The phase
velocity ![]() is fixed for every point
is fixed for every point ![]() . If
. If ![]() ,
then at every
,
then at every ![]() a one-dimensional set of velocities may be
chosen using
a one-dimensional set of velocities may be
chosen using ![]() . This implies that the direction is fixed, but the
magnitude is chosen using
. This implies that the direction is fixed, but the
magnitude is chosen using ![]() . In general, the set of allowable
velocities at a point
. In general, the set of allowable
velocities at a point
![]() is an
is an ![]() -dimensional linear
subspace of the tangent space
-dimensional linear
subspace of the tangent space
![]() (if
(if ![]() is nonsingular).
is nonsingular).
In spite of (13.37), it may still be possible to reach all of the state space from any initial state. It may be costly, however, to reach a nearby point because of the restriction on the tangent space; it is impossible to command a velocity in some directions. For the case of nonlinear systems, it is sometimes possible to quickly reach any point in a small neighborhood of a state, while remaining in a small region around the state. Such issues fall under the general topic of controllability, which will be covered in Sections 15.1.3 and 15.4.3.
Although not covered here, the observability of the system is an important topic in control
[192,478]. In terms of the I-space concepts of Chapter
11, this means that a sensor of the form ![]() is
defined, and the task is to determine the current state, given the
history I-state. If the system is observable, this means that the
nondeterministic I-state is a single point. Otherwise, the system may
only be partially observable. In the case of linear systems, if the
sensing model is also linear,
is
defined, and the task is to determine the current state, given the
history I-state. If the system is observable, this means that the
nondeterministic I-state is a single point. Otherwise, the system may
only be partially observable. In the case of linear systems, if the
sensing model is also linear,
As in the case of discrete planning problems, it is possible to define differential models that depend on time. In the discrete case, this involves a dependency on stages. For the continuous-stage case, a time-varying linear system is defined as
Steven M LaValle 2012-04-20