


Next: Vector fields
Up: Vector Fields and Distributions
Previous: Vector Fields and Distributions
Most of the concepts in this chapter are developed under the
assumption that the state transition equation, 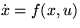 has
the following form:
has
the following form:
| 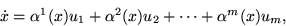 |
(1) |
in which each 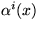 is a vector-valued function of x, and
m is the dimension of U (or the number of inputs). The
is a vector-valued function of x, and
m is the dimension of U (or the number of inputs). The 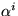 functions can also be arranged in an
functions can also be arranged in an 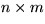 matrix,
matrix,
![\begin{displaymath}
A(x) = [ \alpha^1(x) \;\; \alpha^2(x) \;\; \cdots \;\; \alpha^m(x) ] .\end{displaymath}](img6.gif)
In this case, the state transition equation can be expressed as
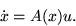
For the rest of the chapter, it will be assumed that the matrix A(x)
is nonsingular. In other words, the rows of A(x) are linearly
independent for all x. To determine if A(x) is nonsingular, one
must find at least one 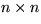 cofactor (or submatrix) of A(x)
which has a nonzero determinant.
cofactor (or submatrix) of A(x)
which has a nonzero determinant.
Steven M. LaValle
8/29/2001
![]() has
the following form:
has
the following form:
![]()
![]()