
Next: Vector fields and velocity Up: 8.3.2 Smooth Manifolds Previous: Coordinates and parameterizations
Now consider defining tangent spaces on manifolds. Intuitively, the
tangent space ![]() at a point
at a point ![]() on an
on an ![]() -dimensional manifold
-dimensional manifold
![]() is an
is an ![]() -dimensional hyperplane in
-dimensional hyperplane in
![]() that best approximates
that best approximates
![]() around
around ![]() , when the hyperplane origin is translated to
, when the hyperplane origin is translated to ![]() . This
is depicted in Figure 8.8. The notion of a tangent was
actually used in Section 7.4.1 to describe local motions
for motion planning of closed kinematic chains (see Figure
7.22).
. This
is depicted in Figure 8.8. The notion of a tangent was
actually used in Section 7.4.1 to describe local motions
for motion planning of closed kinematic chains (see Figure
7.22).
To define a tangent space on a manifold, we first consider a more
complicated definition of the tangent space at a point in
![]() , in
comparison to what was given in Section 8.3.1. Suppose
that
, in
comparison to what was given in Section 8.3.1. Suppose
that
![]() , and consider taking directional derivatives of a
smooth function
, and consider taking directional derivatives of a
smooth function
![]() at a point
at a point
![]() .
For some (unnormalized) direction vector,
.
For some (unnormalized) direction vector,
![]() , the
directional derivative of
, the
directional derivative of ![]() at
at ![]() can be defined as
can be defined as
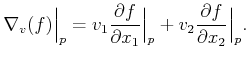 |
(8.31) |
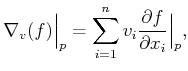 |
(8.32) |
Now consider taking (unnormalized) directional derivatives of a smooth
function,
![]() , on a manifold. For an
, on a manifold. For an
![]() -dimensional manifold, the tangent space
-dimensional manifold, the tangent space ![]() at a point
at a point ![]() can be considered once again as the set of all unnormalized
directions. These directions must intuitively be tangent to the
manifold, as depicted in Figure 8.8. There exists a
clever way to define them without even referring to specific
coordinate neighborhoods. This leads to a definition of
can be considered once again as the set of all unnormalized
directions. These directions must intuitively be tangent to the
manifold, as depicted in Figure 8.8. There exists a
clever way to define them without even referring to specific
coordinate neighborhoods. This leads to a definition of ![]() that
is intrinsic to the manifold.
that
is intrinsic to the manifold.
At this point, you may accept that ![]() is an
is an ![]() -dimensional
vector space that is affixed to
-dimensional
vector space that is affixed to ![]() at
at ![]() and oriented as shown in
Figure 8.8. For the sake of completeness, however, a
technical definition of
and oriented as shown in
Figure 8.8. For the sake of completeness, however, a
technical definition of ![]() from differential geometry will be
given; more details appear in [133,872]. The construction
is based on characterizing the set of all possible directional
derivative operators. Let
from differential geometry will be
given; more details appear in [133,872]. The construction
is based on characterizing the set of all possible directional
derivative operators. Let
![]() denote the set of all smooth
functions that have domains that include
denote the set of all smooth
functions that have domains that include ![]() . Now make the following
identification. Any two functions
. Now make the following
identification. Any two functions
![]() are defined
to be equivalent if there exists an open set
are defined
to be equivalent if there exists an open set
![]() such
that for any
such
that for any ![]() ,
,
![]() . There is no need to
distinguish equivalent functions because their derivatives must be the
same at
. There is no need to
distinguish equivalent functions because their derivatives must be the
same at ![]() . Let
. Let
![]() denote
denote ![]() under this
identification. A directional derivative operator at
under this
identification. A directional derivative operator at ![]() can be
considered as a function that maps from
can be
considered as a function that maps from
![]() to
to
![]() for some
direction. In the case of
for some
direction. In the case of
![]() , the operator appears as
, the operator appears as ![]() for each direction
for each direction ![]() . Think about the set of all directional
derivative operators that can be made. Each one must assign a real
value to every function in
. Think about the set of all directional
derivative operators that can be made. Each one must assign a real
value to every function in
![]() , and it must obey two axioms
from calculus regarding directional derivatives. Let
, and it must obey two axioms
from calculus regarding directional derivatives. Let ![]() denote a directional derivative operator at some
denote a directional derivative operator at some ![]() (be
careful, however, because here
(be
careful, however, because here ![]() is not explicitly represented since
there are no coordinates). The directional derivative operator must
satisfy two axioms:
is not explicitly represented since
there are no coordinates). The directional derivative operator must
satisfy two axioms:
It is helpful, however, to have an explicit way to express vectors in
![]() . A basis for the tangent space can be obtained by using
coordinate neighborhoods. An important theorem from differential
geometry states that if
. A basis for the tangent space can be obtained by using
coordinate neighborhoods. An important theorem from differential
geometry states that if
![]() is a diffeomorphism onto
an open set
is a diffeomorphism onto
an open set
![]() , then the tangent space,
, then the tangent space, ![]() , is
isomorphic to
, is
isomorphic to
![]() . This means that by using a
parameterization (the inverse of a coordinate neighborhood), there is
a bijection between velocity vectors in
. This means that by using a
parameterization (the inverse of a coordinate neighborhood), there is
a bijection between velocity vectors in ![]() and velocity vectors
in
and velocity vectors
in
![]() . Small perturbations in the parameters cause motions
in the tangent directions on the manifold
. Small perturbations in the parameters cause motions
in the tangent directions on the manifold ![]() . Imagine, for example,
making a small perturbation to three quaternion parameters that are
used to represent
. Imagine, for example,
making a small perturbation to three quaternion parameters that are
used to represent ![]() . If the perturbation is small enough,
motions that are tangent to
. If the perturbation is small enough,
motions that are tangent to ![]() occur. In other words, the
perturbed matrices will lie very close to
occur. In other words, the
perturbed matrices will lie very close to ![]() (they will not lie
in
(they will not lie
in ![]() because
because ![]() is defined by nonlinear constraints on
is defined by nonlinear constraints on
![]() , as discussed in Section 4.1.2).
, as discussed in Section 4.1.2).
Now consider different ways to express the tangent space at some point
![]() , other than the poles (a change of coordinates is needed
to cover these). Using the coordinates
, other than the poles (a change of coordinates is needed
to cover these). Using the coordinates
![]() , velocities
can be defined as vectors in
, velocities
can be defined as vectors in
![]() . We can imagine moving in the
plane defined by
. We can imagine moving in the
plane defined by ![]() and
and ![]() , provided that the limits
, provided that the limits
![]() and
and
![]() are respected.
are respected.
We can also use the parameterization to derive basis vectors for the
tangent space as vectors in
![]() . Since the tangent space has
only two dimensions, we must obtain a plane that is ``tangent'' to the
sphere at
. Since the tangent space has
only two dimensions, we must obtain a plane that is ``tangent'' to the
sphere at ![]() . These can be found by taking derivatives. Let
. These can be found by taking derivatives. Let
![]() be denoted as
be denoted as
![]() ,
,
![]() , and
, and
![]() . Two basis vectors for the tangent plane at
. Two basis vectors for the tangent plane at ![]() are
are
![$\displaystyle \left[\frac{dx(\theta,\phi)}{d\theta} \;\;\; \frac{dy(\theta,\phi)}{d\theta} \;\;\; \frac{dz(\theta,\phi)}{d\theta} \right]$](img3132.gif) |
(8.35) |
![$\displaystyle \left[\frac{dx(\theta,\phi)}{d\phi} \;\;\; \frac{dy(\theta,\phi)}{d\phi} \;\;\; \frac{dz(\theta,\phi)}{d\phi} \right] .$](img3133.gif) |
(8.36) |
The tangent vectors can now be imagined as lying in a plane that is
tangent to the surface, as shown in Figure 8.8. The
normal vector to a surface specified as
![]() is
is ![]() ,
which yields
,
which yields
![]() after normalizing. This could
alternatively be obtained by taking the cross product of the two
vectors above and using the parameterization
after normalizing. This could
alternatively be obtained by taking the cross product of the two
vectors above and using the parameterization ![]() to express it in
terms of
to express it in
terms of ![]() ,
, ![]() , and
, and ![]() . For a point
. For a point
![]() , the
plane equation is
, the
plane equation is
| (8.37) |
Steven M LaValle 2012-04-20