
Next: Tangent spaces on manifolds Up: 8.3.2 Smooth Manifolds Previous: 8.3.2 Smooth Manifolds
For any open set
![]() and function
and function
![]() such that
such that ![]() is a homeomorphism onto a subset of
is a homeomorphism onto a subset of
![]() , the pair
, the pair ![]() is called a coordinate neighborhood
(or chart in some literature). The values
is called a coordinate neighborhood
(or chart in some literature). The values ![]() for some
for some ![]() are called the coordinates of
are called the coordinates of ![]() .
.
Let
![]() (the range of
(the range of ![]() ) for some coordinate
neighborhood
) for some coordinate
neighborhood ![]() . Since
. Since ![]() and
and ![]() are homeomorphic via
are homeomorphic via
![]() , the inverse function
, the inverse function ![]() can also be defined. It
turns out that the inverse is the familiar idea of a
parameterization. Continuing Example 8.11,
can also be defined. It
turns out that the inverse is the familiar idea of a
parameterization. Continuing Example 8.11,
![]() yields the mapping
yields the mapping
![]() , which is the familiar parameterization of
the circle but restricted to
, which is the familiar parameterization of
the circle but restricted to
![]() .
.
![]()
To make differentiation work at a point ![]() , it will be
important to have a coordinate neighborhood defined over an open
subset of
, it will be
important to have a coordinate neighborhood defined over an open
subset of ![]() that contains
that contains ![]() . This is mainly because defining
derivatives of a function at a point requires that an open set exists
around the point. If the coordinates appear to have no boundary, then
this will be possible. It is unfortunately not possible to cover all
of
. This is mainly because defining
derivatives of a function at a point requires that an open set exists
around the point. If the coordinates appear to have no boundary, then
this will be possible. It is unfortunately not possible to cover all
of ![]() with a single coordinate neighborhood, unless
with a single coordinate neighborhood, unless
![]() (or
(or
![]() is at least homeomorphic to
is at least homeomorphic to
![]() ). We must therefore define
multiple neighborhoods for which the domains cover all of
). We must therefore define
multiple neighborhoods for which the domains cover all of ![]() .
Since every domain is an open set, some of these domains must
overlap. What happens in this case? We may have two or more
alternative coordinates for the same point. Moving from one set of
coordinates to another is the familiar operation used in calculus
called a change of coordinates. This will now be formalized.
.
Since every domain is an open set, some of these domains must
overlap. What happens in this case? We may have two or more
alternative coordinates for the same point. Moving from one set of
coordinates to another is the familiar operation used in calculus
called a change of coordinates. This will now be formalized.
Suppose that ![]() and
and ![]() are coordinate neighborhoods on
some manifold
are coordinate neighborhoods on
some manifold ![]() , and
, and
![]() . Figure
8.9 indicates how to change coordinates from
. Figure
8.9 indicates how to change coordinates from ![]() to
to ![]() . This change of coordinates is expressed using function
composition as
. This change of coordinates is expressed using function
composition as
![]() (
(![]() maps from
maps from
![]() into
into ![]() , and
, and ![]() maps from a subset
of
maps from a subset
of ![]() to
to
![]() ).
).
We can construct another coordinate function
![]() by using quaternions. This may appear to be a problem because
quaternions have four components; however, the fourth component can be
determined from the other three. Using (4.24) to
(4.26), the
by using quaternions. This may appear to be a problem because
quaternions have four components; however, the fourth component can be
determined from the other three. Using (4.24) to
(4.26), the ![]() ,
, ![]() , and
, and ![]() coordinates can be
determined.
coordinates can be
determined.
Now suppose that we would like to change from Euler angles to
quaternions in the overlap region ![]() , in which
, in which ![]() is an open
set on which the coordinate neighborhood for quaternions is defined.
The task is to construct a change of coordinates,
is an open
set on which the coordinate neighborhood for quaternions is defined.
The task is to construct a change of coordinates,
![]() . We first have to invert
. We first have to invert ![]() over
over ![]() . This means that
we instead need a parameterization of
. This means that
we instead need a parameterization of ![]() in terms of Euler angles.
This is given by (3.42), which yields a rotation matrix,
in terms of Euler angles.
This is given by (3.42), which yields a rotation matrix,
![]() for
for ![]() ,
, ![]() , and
, and
![]() . Once this matrix is determined, then
. Once this matrix is determined, then ![]() can be applied
to it to determine the quaternion parameters,
can be applied
to it to determine the quaternion parameters, ![]() ,
, ![]() , and
, and ![]() . This
means that we have constructed three real-valued functions,
. This
means that we have constructed three real-valued functions, ![]() ,
,
![]() , and
, and ![]() , which yield
, which yield
![]() ,
,
![]() , and
, and
![]() .
Together, these define
.
Together, these define
![]() .
.
![]()
There are several reasons for performing coordinate changes in various
contexts. Example 8.12 is motivated by a change that
frequently occurs in motion planning. Imagine, for example, that a
graphics package displays objects using quaternions, but a
collision-detection algorithm uses Euler angles. It may be necessary
in such cases to frequently change coordinates. From studies of
calculus, you may recall changing coordinates to simplify an integral.
In the definition of a smooth manifold, another motivation arises.
Since coordinate neighborhoods are based on homeomorphisms of open
sets, several may be required just to cover all of ![]() . For example,
even if we decide to use quaternions for
. For example,
even if we decide to use quaternions for ![]() , several coordinate
neighborhoods that map to quaternions may be needed. On the
intersections of their domains, a change of coordinates is necessary.
, several coordinate
neighborhoods that map to quaternions may be needed. On the
intersections of their domains, a change of coordinates is necessary.
Now we are ready to define a smooth manifold. Changes of coordinates
will appear in the manifold definition, and they must satisfy a
smoothness condition. A smooth structure8.5 on a (topological) manifold ![]() is a
family8.6
is a
family8.6
![]() of coordinate neighborhoods such that:
of coordinate neighborhoods such that:
A manifold, as defined in Section 4.1.2, together with a smooth structure is called a smooth manifold.8.8
| (8.22) |
| (8.23) |
| (8.24) |
| (8.25) |
 |
(8.26) |
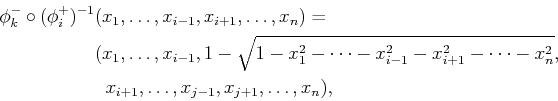 |
(8.27) |
The smooth structure can alternatively be defined using only two
coordinate neighborhoods by using stereographic projection. For
![]() , one coordinate function maps almost every point
, one coordinate function maps almost every point
![]() to
to
![]() by drawing a ray from the north pole to
by drawing a ray from the north pole to ![]() and mapping to
the point in the
and mapping to
the point in the ![]() plane that is crossed by the ray. The only
excluded point is the north pole itself. A similar mapping can be
constructed from the south pole.
plane that is crossed by the ray. The only
excluded point is the north pole itself. A similar mapping can be
constructed from the south pole.
![]()
A smooth structure can be specified by only ![]() coordinate
neighborhoods. For each
coordinate
neighborhoods. For each ![]() from
from ![]() to
to ![]() , let
, let
| (8.28) |
| (8.29) |
A smooth structure over ![]() can be derived as a special case
because
can be derived as a special case
because ![]() is topologically equivalent to
is topologically equivalent to
![]() . Suppose
elements of
. Suppose
elements of ![]() are expressed using unit quaternions. Each
are expressed using unit quaternions. Each
![]() is considered as a point on
is considered as a point on
![]() . There are four
coordinate neighborhoods. For example, one of them is
. There are four
coordinate neighborhoods. For example, one of them is
| (8.30) |
Steven M LaValle 2012-04-20