
Next: Simple projection sensors Up: 11.5.1 Sensor Models Previous: 11.5.1 Sensor Models
Developed mainly in control theory literature, linear sensing
models are some of the most common and important. For all of the
sensors in this family, assume that
![]() (nonsingular
linear transformations allow the sensor space to effectively have
lower dimension, if desired). The simplest case in this family is the
identity sensor, in which
(nonsingular
linear transformations allow the sensor space to effectively have
lower dimension, if desired). The simplest case in this family is the
identity sensor, in which ![]() . In this case, the state
is immediately known. If this sensor is available at every stage,
then the I-space collapses to
. In this case, the state
is immediately known. If this sensor is available at every stage,
then the I-space collapses to ![]() by the I-map
by the I-map
![]() .
.
 |
Now nature sensing actions can be used to corrupt this perfect
state observation to obtain
![]() . Suppose that
. Suppose that
![]() is an estimate of
is an estimate of ![]() , the current state, with error bounded by a
constant
, the current state, with error bounded by a
constant
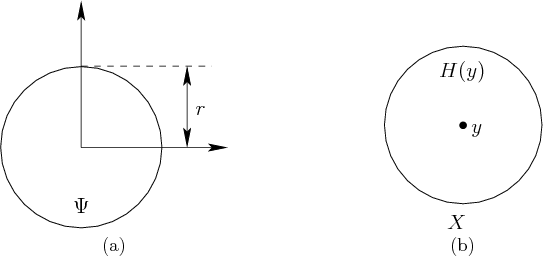
![]() . This can be modeled by assigning for
every
. This can be modeled by assigning for
every ![]() ,
, ![]() as a closed ball of radius
as a closed ball of radius ![]() , centered at
the origin:
, centered at
the origin:
A more typical probabilistic sensing model can be made by letting
![]() and defining a probability density function over
all of
and defining a probability density function over
all of
![]() . (Note that the nondeterministic version of this
sensor is completely useless.) One of the easiest choices to work
with is the multivariate Gaussian probability density function,
. (Note that the nondeterministic version of this
sensor is completely useless.) One of the easiest choices to work
with is the multivariate Gaussian probability density function,
The sensing models presented so far can be generalized by applying
linear transformations. For example, let ![]() denote a nonsingular
denote a nonsingular
![]() matrix with real-valued entries. If the sensor mapping is
matrix with real-valued entries. If the sensor mapping is
![]() , then the state can still be determined immediately
because the mapping
, then the state can still be determined immediately
because the mapping ![]() is bijective; each
is bijective; each ![]() contains a
unique point of
contains a
unique point of ![]() . A linear transformation can also be formed on
the nature sensing action. Let
. A linear transformation can also be formed on
the nature sensing action. Let ![]() denote an
denote an
![]() matrix.
The sensor mapping is
matrix.
The sensor mapping is
| (11.70) |
In general, ![]() and
and ![]() may even be singular, and a linear sensing
model is still obtained. Suppose that
may even be singular, and a linear sensing
model is still obtained. Suppose that ![]() . If
. If ![]() is singular,
however, it is impossible to infer the state directly from a single
sensor observation. This generally corresponds to a projection from
an
is singular,
however, it is impossible to infer the state directly from a single
sensor observation. This generally corresponds to a projection from
an ![]() -dimensional state space to a subset of
-dimensional state space to a subset of ![]() whose dimension is the
rank of
whose dimension is the
rank of ![]() . For example, if
. For example, if
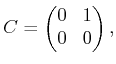 |
(11.71) |
Steven M LaValle 2012-04-20