
Next: 12.4.3 Other Variations Up: 12.4 Visibility-Based Pursuit-Evasion Previous: 12.4.1 Problem Formulation
Now consider designing a complete algorithm that solves the problem in the case of a single pursuer. To be complete, it must find a solution if one exists; otherwise, it correctly reports that no solution is possible. Recall from Figure 12.38 that the nondeterministic I-state changed in an interesting way only after a critical boundary was crossed. The pursuit-evasion problem can be solved by carefully analyzing all of the cases in which these critical changes can occur. It turns out that these are exactly the same cases as considered in Section 12.3.4: crossing inflection rays and bitangent rays. Figure 12.38 is an example of crossing an inflection ray. Figure 12.41 indicates the connection between the gaps of Section 12.3.4 and the parts of the environment that may contain the evader.
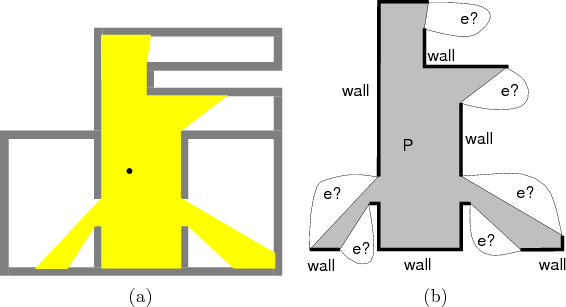 |
Recall that the shadow region is the set of all points not visible
from some ![]() ; this is expressed as
; this is expressed as
![]() . Every
critical event changes the number of shadow components. If an
inflection ray is crossed, then a shadow component either appears or
disappears, depending on the direction. If a bitangent ray is
crossed, then either two components merge into one or one component
splits into two. To keep track of the nondeterministic I-state, it
must be determined whether each component of the shadow region is cleared, which means it certainly does not
contain the evader, or contaminated,
which means that it might contain the evader. Initially, all
components are labeled as contaminated, and as the pursuer moves,
cleared components can emerge. Solving the pursuit-evasion problem
amounts to moving the pursuer until all shadow components are cleared.
At this point, it is known that there are no places left where the
evader could be hiding.
. Every
critical event changes the number of shadow components. If an
inflection ray is crossed, then a shadow component either appears or
disappears, depending on the direction. If a bitangent ray is
crossed, then either two components merge into one or one component
splits into two. To keep track of the nondeterministic I-state, it
must be determined whether each component of the shadow region is cleared, which means it certainly does not
contain the evader, or contaminated,
which means that it might contain the evader. Initially, all
components are labeled as contaminated, and as the pursuer moves,
cleared components can emerge. Solving the pursuit-evasion problem
amounts to moving the pursuer until all shadow components are cleared.
At this point, it is known that there are no places left where the
evader could be hiding.
If the pursuer crosses an inflection ray and a new shadow component appears, it must always be labeled as cleared because this is a portion of the environment that was just visible. If the pursuer crosses a bitangent ray and a split occurs, then the labels are distributed across the two components: A contaminated shadow component splits into two contaminated components, and a cleared component splits into two cleared components. If the bitangent ray is crossed in the other direction, resulting in a merge of components, then the situation is more complicated. If one component is cleared and the other is contaminated, then the merged component is contaminated. The merged component may only be labeled as cleared if both of the original components are already cleared. Note that among the four critical cases, only the merge has the potential to undo the work of the pursuer. In other words, it may lead to recontamination.
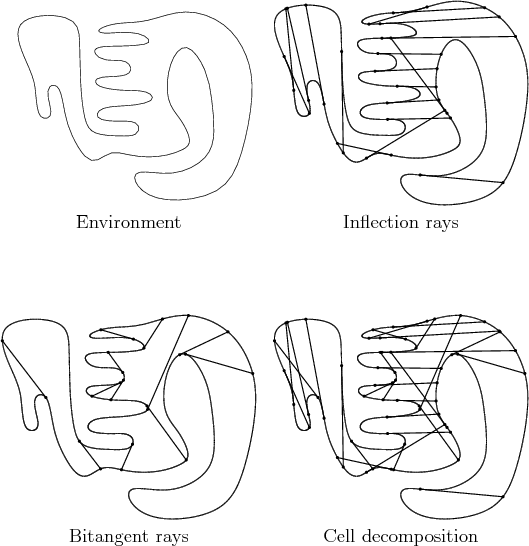 |
Consider decomposing ![]() into cells based on inflection rays and
bitangent rays, as shown in Figure 12.42. These cells
have the following information-conservative property: If the
pursuer travels along any loop path that stays within a 2D cell, then
the I-state remains the same upon returning to the start.
This implies that the particular path taken by the pursuer through a
cell is not important. A solution to the pursuit-evasion problem can
be described as a sequence of adjacent 2D cells that must be visited.
Due to the information-conservative property, the particular path
through a sequence of cells can be chosen arbitrarily.
into cells based on inflection rays and
bitangent rays, as shown in Figure 12.42. These cells
have the following information-conservative property: If the
pursuer travels along any loop path that stays within a 2D cell, then
the I-state remains the same upon returning to the start.
This implies that the particular path taken by the pursuer through a
cell is not important. A solution to the pursuit-evasion problem can
be described as a sequence of adjacent 2D cells that must be visited.
Due to the information-conservative property, the particular path
through a sequence of cells can be chosen arbitrarily.
Searching the cells for a solution is more complicated than searching
for paths in Chapter 6 because the search must be
conducted in the I-space. The pursuer may visit the same cell in ![]() on different occasions but with different knowledge about which
components are cleared and contaminated. A directed graph,
on different occasions but with different knowledge about which
components are cleared and contaminated. A directed graph,
![]() , can
be constructed as follows. For each 2D cell in
, can
be constructed as follows. For each 2D cell in ![]() and each possible
labeling of shadow components, a vertex is defined in
and each possible
labeling of shadow components, a vertex is defined in
![]() . For
example, if the shadow region of a cell has three components, then
there are
. For
example, if the shadow region of a cell has three components, then
there are ![]() corresponding vertices in
corresponding vertices in
![]() . An edge exists
in
. An edge exists
in
![]() between two vertices if: 1) their corresponding cells are
adjacent, and 2) the labels of the components are consistent with the
changes induced by crossing the boundary between the two cells. The
second condition means that the labeling rules for an appear,
disappear, split, or merge must be followed. For example, if crossing
the boundary causes a split of a contaminated shadow component, then
the new components must be labeled contaminated and all other
components must retain the same label. Note that
between two vertices if: 1) their corresponding cells are
adjacent, and 2) the labels of the components are consistent with the
changes induced by crossing the boundary between the two cells. The
second condition means that the labeling rules for an appear,
disappear, split, or merge must be followed. For example, if crossing
the boundary causes a split of a contaminated shadow component, then
the new components must be labeled contaminated and all other
components must retain the same label. Note that
![]() is directed
because many motions in the
is directed
because many motions in the
![]() are not reversible. For
example, if a contaminated region disappears, it cannot reappear as
contaminated by reversing the path. Note that the information in this
directed graph does not improve monotonically as in the case of lazy
discrete localization from Section 12.2.1. In the current
setting, information is potentially worse when shadow components merge
because contamination can spread.
are not reversible. For
example, if a contaminated region disappears, it cannot reappear as
contaminated by reversing the path. Note that the information in this
directed graph does not improve monotonically as in the case of lazy
discrete localization from Section 12.2.1. In the current
setting, information is potentially worse when shadow components merge
because contamination can spread.
To search
![]() , start with any vertex for which all shadow
region components are labeled as contaminated. The particular
starting cell is not important. Any of the search algorithms from
Section 2.2 may be applied to find a goal vertex, which
is any vertex of
, start with any vertex for which all shadow
region components are labeled as contaminated. The particular
starting cell is not important. Any of the search algorithms from
Section 2.2 may be applied to find a goal vertex, which
is any vertex of
![]() for which all shadow components are
labeled as cleared. If no such vertices are reachable from the
initial state, then the algorithm can correctly declare that no
solution exists. If a goal vertex is found, then the path in
for which all shadow components are
labeled as cleared. If no such vertices are reachable from the
initial state, then the algorithm can correctly declare that no
solution exists. If a goal vertex is found, then the path in
![]() gives the sequence of cells that must be visited to solve
the problem. The actual path through
gives the sequence of cells that must be visited to solve
the problem. The actual path through ![]() is then constructed from the
sequence of cells. Some of the cells may not be convex; however,
their shape is simple enough that a sophisticated motion planning
algorithm is not needed to construct a path that traverses the cell
sequence.
is then constructed from the
sequence of cells. Some of the cells may not be convex; however,
their shape is simple enough that a sophisticated motion planning
algorithm is not needed to construct a path that traverses the cell
sequence.
The algorithm presented here is conceptually straightforward and
performs well in practice; however, its worst-case running time is
exponential in the number of inflection rays. Consider a polygonal
environment that is expressed with ![]() edges. There can be as many as
edges. There can be as many as
![]() inflections and
inflections and ![]() bitangents. The number of cells is
bounded by
bitangents. The number of cells is
bounded by ![]() [412]. Unfortunately,
[412]. Unfortunately,
![]() has an
exponential number of vertices because there can be as many as
has an
exponential number of vertices because there can be as many as ![]() shadow components, and there are
shadow components, and there are ![]() possible labelings if there
are
possible labelings if there
are ![]() components. Note that
components. Note that
![]() does not need to be computed
prior to the search. It can be revealed incrementally during the
planning process. The most efficient complete algorithm, which is
more complicated, solves the pursuit-evasion problem in time
does not need to be computed
prior to the search. It can be revealed incrementally during the
planning process. The most efficient complete algorithm, which is
more complicated, solves the pursuit-evasion problem in time ![]() and was derived by first proving that any problem that can be solved
by a pursuer using the visibility polygon can be solved by a pursuer
that uses only two beams of light [770]. This simplifies
and was derived by first proving that any problem that can be solved
by a pursuer using the visibility polygon can be solved by a pursuer
that uses only two beams of light [770]. This simplifies
![]() from a 2D region in
from a 2D region in ![]() to two rotatable rays that emanate
from
to two rotatable rays that emanate
from ![]() and dramatically reduces the complexity of the I-space.
and dramatically reduces the complexity of the I-space.
Steven M LaValle 2012-04-20