As for a single rigid body, the 3D case is significantly more
complicated than 2D due to 3D rotations. Also, several more types of
joints are possible, as shown in Figure 2.10.
Nevertheless, it is naturally extend the ideas from transformations of
2D kinematic chains to the 3D case. The following steps from Section
2.3.1 will be recycled here: 1) the coordinate frame must be
carefully placed to define the model for each ![]() ; 2) based on
joint relationships, several parameters will be defined; 3) the
parameters will be used to define a homogeneous transformation matrix,
Ti; 4) the transformation of points on link
; 2) based on
joint relationships, several parameters will be defined; 3) the
parameters will be used to define a homogeneous transformation matrix,
Ti; 4) the transformation of points on link ![]() will be given by
will be given by
![]() .
.
Consider a kinematic chain of m links in ![]() , in which each
, in which each
![]() for
for ![]() is attached to
is attached to ![]() by a revolute
joint. Each link can be a complicated, rigid body as shown in Figure
2.11.a. For the 2D problem, the coordinate frames were based
on the points of attachment. For the 3D problem, it is convenient to
use the axis of rotation of each revolute joint (this is equivalent to
the point of attachment for the 2D case). The axes of rotation will
generally be skew lines in
by a revolute
joint. Each link can be a complicated, rigid body as shown in Figure
2.11.a. For the 2D problem, the coordinate frames were based
on the points of attachment. For the 3D problem, it is convenient to
use the axis of rotation of each revolute joint (this is equivalent to
the point of attachment for the 2D case). The axes of rotation will
generally be skew lines in ![]() , as shown in Figure
2.11.b. Let Zi refer to the axis of rotation for the
revolute joint that holds
, as shown in Figure
2.11.b. Let Zi refer to the axis of rotation for the
revolute joint that holds ![]() to
to ![]() . Between each pair of
axes in succession, draw a vector, Xi, that joins the two closest
pair of points, one from Zi and the other from Zi-1 (this
choice is unique if the axes are not parallel). The recommended
coordinate frame for defining the geometric model for each
. Between each pair of
axes in succession, draw a vector, Xi, that joins the two closest
pair of points, one from Zi and the other from Zi-1 (this
choice is unique if the axes are not parallel). The recommended
coordinate frame for defining the geometric model for each ![]() will
be given with respect to Zi and Xi, which are given in Figure
2.11.b. Assuming a right-handed coordinate system, the Yi axis
points away from us in Figure 2.11.b. In the
transformations that appear shortly, the coordinate frame given by
Xi, Yi, and Zi, will be most convenient for defining the
model for
will
be given with respect to Zi and Xi, which are given in Figure
2.11.b. Assuming a right-handed coordinate system, the Yi axis
points away from us in Figure 2.11.b. In the
transformations that appear shortly, the coordinate frame given by
Xi, Yi, and Zi, will be most convenient for defining the
model for ![]() , even if the origin of the frame lies outside of
, even if the origin of the frame lies outside of
![]() .
.
In Section 2.3.1, each Ti was defined in terms of two
parameters, ai-1 and ![]() . For the 3D case, four
parameters will be defined: di,
. For the 3D case, four
parameters will be defined: di, ![]() , ai-1, and
, ai-1, and
![]() . These are referred to as Denavit-Hartenberg
parameters, or DH parameters for short [2]. The
definition of each parameter is indicated in Figure 2.12.
Figure 2.12.a shows the definition of di. Note that
Xi-1 and Xi contact Zi at two different places. Let di
denote signed distance between these points of contact. If Xi is
above Xi-1 along Zi, then di is positive; otherwise, di
is negative. The parameter
. These are referred to as Denavit-Hartenberg
parameters, or DH parameters for short [2]. The
definition of each parameter is indicated in Figure 2.12.
Figure 2.12.a shows the definition of di. Note that
Xi-1 and Xi contact Zi at two different places. Let di
denote signed distance between these points of contact. If Xi is
above Xi-1 along Zi, then di is positive; otherwise, di
is negative. The parameter ![]() is the angle between Xi and
Xi-1, which corresponds to the rotation about Zi that moves
Xi-1 to coincide Xi. In Figure 2.12.b, Zi is
pointing outward. The parameter ai is the distance between Zi
and Zi-1; recall these are generally skew lines in
is the angle between Xi and
Xi-1, which corresponds to the rotation about Zi that moves
Xi-1 to coincide Xi. In Figure 2.12.b, Zi is
pointing outward. The parameter ai is the distance between Zi
and Zi-1; recall these are generally skew lines in ![]() . The
parameter
. The
parameter ![]() is the angle between Zi and Zi-1. In
Figure 2.12.d, Xi-1 is pointing outward.
is the angle between Zi and Zi-1. In
Figure 2.12.d, Xi-1 is pointing outward.
The homogeneous transformation matrix Ti will be constructed by combining two simpler transformations. The transformation
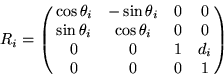
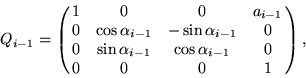
The homogeneous transformation matrix, Ti, for ![]() , is
, is
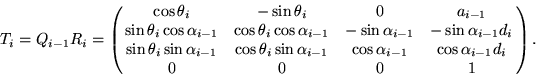 |
(14) |
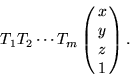
For each revolute joint, ![]() is treated as the only variable in
Ti. A prismatic joints can be simulated by allowing ai to vary.
More complicated joints can be simulated as a sequence of degenerate
joints. For example, a spherical joint can be considered as a
sequence of three zero-length revolute joints; the joints perform a
roll, a pitch, and a yaw. Another option for more complicated joints
is to derive a special homogeneous transformation matrix. This might
be needed to preserve some of the topological properties that will be
discussed in Chapter
is treated as the only variable in
Ti. A prismatic joints can be simulated by allowing ai to vary.
More complicated joints can be simulated as a sequence of degenerate
joints. For example, a spherical joint can be considered as a
sequence of three zero-length revolute joints; the joints perform a
roll, a pitch, and a yaw. Another option for more complicated joints
is to derive a special homogeneous transformation matrix. This might
be needed to preserve some of the topological properties that will be
discussed in Chapter ![]() .
.